TRAVAUX
DU
COMITÉ FRANÇAIS D'HISTOIRE DE LA GÉOLOGIE
- Troisième série -
T.XXI (2007)

Élie de Beaumont (1798-1874), des systèmes de montagnes au réseau pentagonal

Jacques Touret

COMITÉ FRANÇAIS D'HISTOIRE DE LA GÉOLOGIE (COFRHIGEO) (séance du 13 juin 2007)

Résumé.
Pendant la plus grande partie du XIXe siècle, la géologie française a été dominée par la personnalité écrasante de Léonce Élie de Beaumont, inventeur du " réseau pentagonal ". On détaille les principes et l'illustration de ce modèle, premier essai de tectonique globale, dont l'oubli actuel paraît aussi immérité que la confiance aveugle que lui ont accordée bon nombre de ses contemporains.

Mots-clés : réseau pentagonal - chaînes de montagnes - tectonique globale - XIXe siècle

Abstract.
During most of the 19th century, French geology was dominated by the strong personality of Léonce Élie de Beaumont, inventor of the " réseau pentagonal ". The reseau was the first attempt to interpret global tectonics, well before the discovery of plates, and despite fundamental errors it left a significant influence on many subsequent theories, notably geosynclines. Its conception and illustration represent an enormous amount of work, mostly done at the École des mines, whose oblivion today is as unjustified as its blind acceptance at the time of Élie de Beaumont splendour.

Key words: réseau pentagonal - mountain chains - global tectonics - 19th century

 

La bibliothèque de l'École des mines de Paris conserve précieusement quelques globes en carton stuqué de taille modeste : trois petits, d'un diamètre d'une dizaine de centimètres, un sensiblement plus gros, d'un diamètre pratiquement double. Tous sont remarquables par une décoration graphique extrêmement complexe, constituée d'un entrelacs de lignes géométriques de couleurs variées et, pour le plus gros, d'un réseau de fils maintenus par des épingles, de couleurs variées, superposé à un fonds topographique. C'est à peu près tout ce qui subsiste d'un premier essai de synthèse unificatrice de la géométrie des déformations tectoniques à l'échelle de la Terre, le " réseau pentagonal ", qui fut créé par le grand maître de la géologie française du XIXe siècle, Jean-Baptiste-Armand-Louis-Léonce Élie de Beaumont (1798-1874). Première tentative globale d'analyse des formes du relief de la Terre qui, poursuivie par celles d'Eduard Suess et Alfred Wegener, conduira vers la " révolution " de la tectonique des plaques (1).

Une personnalité autoritaire

Cumulant fonctions et honneurs officiels, Élie de Beaumont (Fig. 1) régna en monarque absolu sur la géologie française pendant plus de cinquante ans, aidé par quelques collaborateurs dévoués qui acceptaient volontiers de rester dans l'ombre du maître. Il fut en même temps professeur au Collège de France et à l'École des mines, sans parler, à partir de 1853, des fonctions de secrétaire perpétuel de l'Académie des sciences, qui lui prenaient beaucoup de temps, et, à la fin de sa vie, de sénateur. Bourreau de travail, il fut entouré par un petit cercle de fidèles, dont les rangs s'éclaircirent au fil des années, mais qui lui vouaient une admiration sans bornes. Au Collège de France, ce fut surtout Charles Sainte-Claire Deville (1814-1876), frère du chimiste, plus géophysicien et météorologiste que géologue, qui assura la suppléance de ses cours pendant une quinzaine d'années, avant de devenir, dix-huit mois avant son décès, le professeur titulaire. Il n'aura ainsi que le temps d'assurer un seul cours, entièrement consacré à l'illustration du modèle de son maître. À l'École des mines, Alexandre-Eugène Béguyer de Chancourtois (1820-1886) (2), qui fut son élève, remplaça également pendant longtemps le professeur titulaire, qui ne donnait en personne que la première leçon de son cours de géologie. Comme Charles Sainte-Claire Deville, il dut également attendre la mort de son maître pour devenir professeur de géologie en titre, avec un peu plus de bonheur, puisqu'il lui restait une bonne dizaine d'années à vivre. Mais entre temps il avait occupé de multiples fonctions, jouant un rôle essentiel dans l'aménagement de l'hôtel de Vendôme, où l'École des mines s'était installée en 1816, et, en tant que professeur de topographie, faisant réaliser de multiples objets, en particulier globes ou cartes, indispensables à la compréhension de la pensée du maître.


Fig. 1. Portaits officiels d'Élie de Beaumont. Plus âgé (a), à l'École des mines, plus jeune (b), aux Archives de l'Académie des sciences. La couleur de la cravate change, mais l'expression reste aussi sévère.

La première carte géologique de la France

Élève de l'École des mines de 1820 à 1822, Élie de Beaumont y fut immédiatement considéré comme un sujet d'exception. Déjà auréolé d'un prix de mathématiques du Concours général, obtenu alors qu'il n'avait qu'une quinzaine d'années, il était entré en 1817 second à Polytechnique, pour en sortir major deux ans plus tard et, inaugurant une tradition qui ne s'est guère démentie jusqu'à nos jours, intégrer avec le même rang le Corps des mines. Il semble que ce soit la première fois qu'un major de Polytechnique ait choisi le service des mines, ce qui tendrait à indiquer que, jusque-là, ce service était loin d'avoir la réputation qu'il a acquise depuis auprès des polytechniciens. Le jeune élève ingénieur est alors remarqué par le professeur de géologie, André Brochant de Villiers (1772-1840), qui avait assuré le cours de géologie (3) lorsque l'École avait été décentralisée dans les Alpes sous le Consulat, par un décret signé du Premier consul Bonaparte en personne. Séjour qui dura douze ans, de 1802 et 1814, et qui ne fut pas simple, l'École, qui portait alors le nom d'École pratique des mines du Mont-Blanc, devant trouver ses propres ressources tirées de l'exploitation du plomb argentifère de la mine de Pesey. Tâche qui aurait pu sembler impossible mais qui, grâce au talent des quelques professeurs et surtout du directeur, Jean-Godefroy Schreiber (1746-1827), réussit au-delà de toute espérance. On put non seulement faire vivre l'École - en dépit des récriminations constantes des élèves se plaignant de leurs difficiles conditions d'existence -, mais constituer des réserves qui, de 1814 à 1816, servirent à payer les déménagements successifs de l'École réinstallée dans la capitale, d'abord au Petit-Luxembourg, puis à l'hôtel de Vendôme (6). Le cours de géologie professé par Brochant de Villiers à l'École de Pesey était très complet, orienté vers les applications pratiques et, d'une façon générale, novateur si on le compare aux autres travaux de cette époque. Il part de l'analyse des paysages, pour en déduire l'architecture du bâti souterrain et déterminer la nature et l'âge des roches qui le composent (3, p. 163). On trouve dans ce cours des considérations sur les directions de chaînes de montagnes qui marqueront le jeune Élie de Beaumont et qui l'inciteront, plus tard, à poursuivre dans cette voie. Mais, bien qu'il n'ait pas eu la possibilité de le faire dans les Alpes en raison de la complexité de la région, cette expérience a sans aucun doute convaincu Brochant de Villiers de l'intérêt de consigner les observations de terrain sur des documents immédiatement utilisables. En 1822, il est toujours professeur de géologie et minéralogie (la chaire ne sera dédoublée qu'en 1835) et, (selon Grandchamp, communication écrite), à la demande du directeur général des ponts et chaussées et des mines, il rédige un premier rapport sur la nécessité de faire exécuter la carte géologique de la France. La notion même de carte géologique était alors très nouvelle. Il existait bien quelques embryons de cartes minéralogiques, notamment l'Atlas minéralogique de la France de Jean-Étienne Guettard (1715-1786) (4), commandité dès 1771 par un ministre de Louis XVI. Guettard eut alors comme assistant le jeune Lavoisier, qui réalisa à cette occasion l'un de ses premiers travaux scientifiques. Mais il ne s'agissait guère que de reporter l'emplacement des gisements de substances utiles, sans aucun essai d'interprétation. Travail qui fut du reste interrompu avant d'avoir été mené à son terme, tant en raison des difficultés de la période révolutionnaire que des dissensions qui se firent vite jour entre les auteurs sur ce qui devait figurer sur les cartes. Les terrains sédimentaires, notamment, qui se présentent sous forme de couches régulières, les strates, ont un contour géométrique bien précis, qui lorsqu'il est convenablement représenté sur une surface topographique peut donner à une carte un caractère prédictif, permettant de prévoir par des coupes la nature des terrains en profondeur, dans des domaines qui ne nous sont pas directement accessibles. En 1815, on n'en est pas encore là, mais une étape essentielle a été franchie en Angleterre par un géomètre, William "Strata" Smith (1779-1839) qui, après bien des vicissitudes et de multiples incompréhensions de la part des spécialistes, vient de publier une grande carte (" The Great map ", près de 6 mètres carrés), couvrant une bonne part des îles Britanniques (5). Brochant de Villiers est profondément impressionné par cette carte, ainsi que par celle de George Bellas Greenough (1778-1855) (" jusqu'ici la plus belle carte de ce genre que l'on connaisse ") et conçoit le projet grandiose de réaliser le même travail en France, ce qui va mobiliser toute son énergie jusqu'à sa mort. Il n'a pu toutefois en suivre l'achèvement puisque, par une cruelle ironie de l'histoire, les six feuilles de la Carte géologique de la France au 1/500 000, " publiée sous la direction de M. Brochant de Villiers ", ne paraîtront qu'en 1841.

Les deux principaux auteurs de la carte, Léonce Élie de Beaumont et Ours-Armand Petit-Dufrénoy (1792-1857) sont appelés à une brillante carrière. Dés 1825, Dufrénoy supplée Brochant de Villiers pour le double cours de géologie et de minéralogie, qu'il assurait en titre depuis l'École des Alpes. À partir de 1827, il ne donne plus que le cours de minéralogie, devenant comme Élie de Beaumont professeur titulaire en 1835, par dédoublement de la chaire de Brochant de Villiers. D'après Aguillon (1889, p. 126-127) (6), " la chaire de minéralogie et géologie ne fut officiellement dédoublée […] que lorsque Brochant de Villiers donna sa démission de professeur titulaire en 1835 ; mais toutefois, depuis 1827, les deux cours étaient professés à part : par Dufrénoy pour la minéralogie, et par Elie de Beaumont pour la géologie, tous deux en qualité de professeurs-adjoints de Brochant ". Se déchargeant comme on l'a dit sur quelques fidèles collaborateurs pour l'essentiel de ses tâches d'enseignement, Élie de Beaumont va pendant plus d'un demi-siècle consacrer l'essentiel de ses forces à la résolution d'un grand problème, le mode de formation des chaînes de montagnes. Pendant ce temps Dufrénoy qui, à la suite de René-Just Haüy et Alexandre Brongniart, enseigne la minéralogie au Muséum à partir de 1847, s'occupe plus directement du bon fonctionnement de l'École des mines, dont il sera le directeur de 1848 jusqu'à sa mort. (6)

Les idées d'Élie de Beaumont sur la formation des chaînes de montagnes

Depuis l'Antiquité, l'une des grandes questions que se posaient tous ceux qui s'intéressaient à notre planète concernait la formation des chaînes de montagnes. Les Anciens voyaient dans ces cimes inaccessibles le repaire des Dieux, tandis que Horace-Bénédict de Saussure, à la fin du XVIIIe siècle, tentait une approche plus scientifique. Il pensait que les montagnes les plus hautes faisaient apparaître en surface les terrains les plus anciens, d'où le nom de " protogine ", mère ancestrale, pour le granite du Mont-Blanc. Nom auquel il donnera une popularité durable, mais qui a été utilisé pour la première fois par le chirurgien et naturaliste genevois Louis Jurine (1751-1819). Cette première tentative d'interprétation chronologique de la surrection des chaînes de montagnes sera reprise par Élie de Beaumont, le conduisant à élaborer une théorie qui prendra progressivement forme entre 1829, l'année de sa première note sur les montagnes de l'Oisans (7), et 1852, avec la parution de son " opus magnum ", la célèbre Notice sur les systèmes de montagnes (8). À cette époque, la grande dispute entre neptunistes et plutonistes était à peu près terminée, avec la victoire apparemment totale des idées de James Hutton, mais l'influence du maître de Freiberg restait très marquée à l'École des mines, en raison notamment du caractère appliqué de cet établissement. Brochant de Villiers avait séjourné en Saxe en tant qu'élève de 1791 à 1793, puis en tant que confrère en 1803, afin d'y recueillir des conseils pour la préparation de son cours. Gottlob Werner avait également rendu visite à René-Just Haüy à Paris en 1801, peu de temps avant le départ de l'École pour les Alpes, puis reçu dans son académie quelques élèves parisiens, qui se mêlaient à d'autres, provenant de tous les pays d'Europe. L'un d'entre eux était le chevalier d'Aubuisson de Voisins (1769-1841), qui avait pris du service dans l'armée de Condé et qui, en tant qu'émigré, ne put pendant longtemps revenir en France. Se tournant vers la géologie à l'issue des hostilités, il passe alors quelques années à Freiberg et devient l'un des élèves favoris de Werner. Revenu en France sous Napoléon, mais ayant alors perdu tous ses biens, le Conseil des mines le nomme responsable adjoint des collections, tout en le chargeant de traduire en français les ouvrages allemands qui, à l'époque, faisaient autorité en géologie minière. En 1802, Gottlob Werner envoie l'un de ses autres élèves favoris, Leopold von Buch (1774-1853), visiter la chaîne des Puys, afin de confirmer ses idées sur l'origine neptunienne des basaltes. D'Aubuisson de Voisins le reçoit et l'accompagne sur le terrain. Leopold von Buch, qui avait auparavant visité les volcans actifs du sud de l'Italie, est convaincu des ressemblances profondes entre les deux régions. Il a donc beaucoup de peine à accepter l'explication de Werner, à savoir la combustion en profondeur de gisements de houille, mais, sans doute pour ne pas heurter son maître, il prend soin de dire que cette origine reste valable pour les volcans de Saxe, " puisqu'il n'y a pas à proximité de volcans actifs ". D'Aubuisson de Voisins, qui va bientôt occuper d'importantes fonctions dans l'administration des mines du sud de la France, restera toujours un fidèle défenseur des idées de Werner (9), alors que Leopold von Buch, prenant ses distances, deviendra bientôt un des défenseurs les plus respectés des idées plutonistes. Sa visite des volcans d'Auvergne le met sur la voie d'une hypothèse qui, pense-t-il, lui assurera une célébrité universelle : les cônes volcaniques ne sont pas, comme on le croyait depuis l'Antiquité (et comme l'observation immédiate semble bien le démontrer), créés par la chute des débris envoyé dans l'atmosphère par l'éruption, mais par la poussée du magma sous-jacent, qui déforme les couches affleurant en surface. Sous le nom de " cratères de soulèvement ", cette théorie prend forme à l'occasion de visites de volcans du sud de l'Italie, notamment l'Etna (10), puis, surtout, de ceux des îles Canaries, pour être formulée sous sa forme définitive en 1825 (11), au moment même où Élie de Beaumont commençait ses levers de la Carte géologique de la France.

C'est peu de dire qu'Élie de Beaumont adopte avec enthousiasme les idées de Leopold von Buch. Il recherche avidement tous ses travaux (12), collectionne avec un plaisir manifeste les envois dédicacés de la main de l'auteur et, comme on peut s'en rendre compte tout au long de ses multiples publications, le considère comme son véritable maître. Il faut dire que cette idée des cratères de soulèvement s'accorde bien avec une autre hypothèse qui, là encore, n'est pas d'Élie de Beaumont lui-même, mais qui, conséquence à peu près inéluctable du plutonisme, paraissait à l'époque tellement évidente que, finalement, elle n'avait guère besoin d'être démontrée. Depuis Descartes, la plupart des géologues admettaient que le noyau de la Terre est incandescent, siège du " feu central ". À l'origine, notre planète aurait été une boule de feu, comme le Soleil, mais elle aurait subi un premier refroidissement conduisant à la formation d'une croûte solide. Le refroidissement, se poursuivant, entraînait la contraction du noyau, obligeant la croûte adhérente à se rider pour s'adapter à la diminution de la surface. Volcans et chaînes de montagnes sont donc fondamentalement liés à un même mécanisme, le soulèvement en profondeur de l'écorce par le magma sous-jacent. Ce soulèvement aurait été ponctuel pour les volcans, ménageant, dans le cas des volcans actifs, un passage direct vers le feu central ; au contraire, il aurait été linéaire dans le cas des chaînes de montagnes, disposées le long de grandes fractures rectilignes. Comme dans le cas des volcans actifs, qui surgissent brutalement lors d'une éruption, la fracturation et la structuration des chaînes de montagnes auraient été un phénomène instantané, catastrophique. L'homme n'a pu en avoir connaissance, car aucune surrection ne s'est produite dans la période historique, mais Élie de Beaumont a manifestement à l'esprit une certaine comparaison avec les éruptions volcaniques. Le noyau surgirait brutalement, sur une hauteur de quelques kilomètres (mouvement centrifuge), pendant que l'encaissant s'abaisserait par réaction de quelques dizaines de mètres (mouvement centripète). Pour bien montrer la brutalité du phénomène, il fait appel à ses connaissances militaires - comme la plupart des Polytechniciens, il a un faible pour l'artillerie - et compare ces mouvements à ceux d'un canon au moment de la mise à feu. Toutefois, les roches qui jaillissent au cœur de la fracture ne sont pas un magma brûlant, directement issu du feu central, mais un noyau de " terrains primitifs " (c'est-à-dire de granite), correspondant aux premières roches solidifiées autour du noyau en feu (Fig. 2).


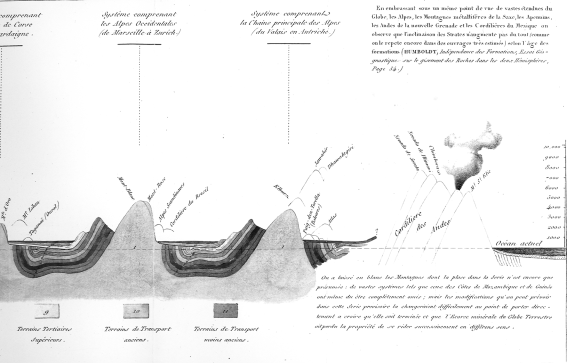
Fig. 2. Structure des chaînes de montagnes, d'après Élie de Beaumont (Notice, planche 3, partiel). L'âge de la surrection se situe entre celui du dernier terrain redressé et du terrain horizontal (pour le système des Alpes, le plus récent de tous, c'est le " terrain de transition plus récent ").

Vieille notion qui transpose directement, en ambiance plutonique, une classification héritée de Werner, et qui mettra bien longtemps à s'effacer puisque, encore aujourd'hui, on y trouve quelques réminiscences dans la " couche granitique ", placée par certains géophysiciens à la base des continents. Pour Élie de Beaumont, les terrains primitifs n'arriveraient pas en surface sous forme de magma fondu, mais ils pourraient, comme lors des éruptions volcaniques, être accompagnés d'une grande quantité de gaz, entraînant la fonte brutale des neiges et glaces accumulées sur les sommets. Bien que la comparaison avec les bouches à feu semble indiquer qu'Élie de Beaumont considérait aussi que la surrection aurait pu projeter des roches à une distance de quelques kilomètres, c'est essentiellement à ce " grand dégel géologique " qu'Élie de Beaumont attribuait le transport des blocs erratiques qui, à cette époque, faisait aussi l'objet de nombreuses discussions (13).

À ces hypothèses qui, après tout, ne faisaient que refléter les idées que la plupart de ses contemporains avaient sur la structure de notre planète, Élie de Beaumont ajoute une dimension chronologique : chaque surrection d'une chaîne de montagne est un phénomène unique, qui se produit simultanément sur toute la Terre avec la même direction, formant un grand cercle à l'échelle du Globe. Inversement, pourrait-on dire, deux directions successives forment un certain angle, souvent proche de 90°, variable dans le détail en fonction des régions considérées. À toutes les époques géologiques, les chaînes gardent la même structure : au centre, un noyau primitif, de composition essentiellement granitique, et, de part et d'autre, des terrains sédimentaires de plus en plus redressés, de plus en plus vieux en se rapprochant du noyau. Une interprétation qu'Horace-Bénédict de Saussure avait déjà pressentie à propos du Mont-Blanc, mais qui peut être désormais généralisée en tenant compte des progrès réalisés par les stratigraphes anglais. L'âge d'une surrection doit se trouver entre celui du terrain redressé le plus jeune et celui du terrain horizontal qui le recouvre : on parlerait aujourd'hui de discordance (Fig. 2). De proche en proche, on peut ainsi établir la chronologie des divers " systèmes de montagne ", terme utilisé par Élie de Beaumont dès ses premières publications (14).


Fig. 3. Expériences de M. Daubrée sur la contraction de ballons souples.

Bien entendu, Élie de Beaumont a conscience de ce que la direction des différents éléments d'une chaîne de montagne est quelque peu variable. En général, on observe des chaînons, d'une longueur moyenne de quelques dizaines de kilomètres, qui ont en gros la même direction, mais sont loin d'être strictement parallèles. Il y a là une difficulté majeure qu'il résout dès ses premières observations, mais qu'il n'explicitera qu'une vingtaine d'années plus tard (8). À la surface de la Terre, les chaînes de montagnes alternent avec des bassins sédimentaires, dans des " fuseaux " d'une largeur maximale de quelque 2 000 kilomètres. Un fuseau contient tous les chaînons d'un même système, même lorsque ceux-ci ne sont pas strictement parallèles. Il peut être matérialisé par son cercle médian, appelé " cercle de comparaison ", qui donnera la direction du système de chaînes à l'échelle planétaire.

Pour illustrer ce mode de formation des reliefs, beaucoup de commentateurs ont utilisé l'image d'une pomme qui se ride, qui n'est pas très appropriée. Élie de Beaumont préférait parler des côtes d'un melon, qui illustrent beaucoup mieux la notion de fuseau. C'est probablement cette représentation qui a donné à Gabriel-Auguste Daubrée (1814-1896), le pionnier de la géologie expérimentale, l'idée de tester l'hypothèse de la contraction par des modèles qui, à vrai dire, nous paraissent aujourd'hui quelque peu simplistes. Dans son laboratoire de l'École des mines, dont, en 1862, il venait d'être nommé directeur, il conçoit un ballon souple rempli d'air, dont la surface est rigidifiée en certains endroits par un enduit. Lorsque l'air s'échappe, fuseaux et bourrelets apparaissent, donnant effectivement une certaine illustration de la pensée d'Élie de Beaumont (Fig. 3). Ce dernier nomme ces bourrelets des " bossellements ", qui jouent un rôle crucial dans son analyse de la contraction terrestre (Notice…, p. 237, cf. Sengör, p. 117 sq.). D'autres expériences concernent des structures circulaires, que Daubrée compare aux cratères lunaires. Or, pour Élie de Beaumont, ces cratères, comme sur Terre, étaient des " cratères d'élévation ", une autre manifestation du soulèvement profond. Le livre de Daubrée relatant ces expériences ne paraîtra qu'en 1879 (15), mais l'auteur prend soin d'indiquer que les expériences ont été réalisées " d'après une idée exposée dès 1833 par Elie de Beaumont dans son cours à l'Ecole des Mines ". Il est donc très vraisemblable que celui-ci en ait eu connaissance, au moins de façon préliminaire, et qu'elles aient pu le confirmer dans la valeur de son analyse.

L'inventaire des systèmes

Sans attendre la vérification et la confirmation de ses idées, ce qui s'étendra sur plusieurs dizaines d'années, Élie de Beaumont se met au travail. Ses premières observations sont présentées oralement devant l'Académie des sciences le 22 juin 1829. Il identifie alors quatre systèmes, respectivement de la Côte d'Or, des Pyrénées, des Alpes occidentales, et de la chaîne principale des Alpes. Sa communication soulève l'enthousiasme des académiciens, notamment celui du secrétaire perpétuel, François Arago (1786-1853), auquel Élie de Beaumont succédera en 1853. Les quatre systèmes sont repris dans le rapport d'Arago pour l'année académique 1830, inséré dans l'Annuaire du Bureau des longitudes (16). Entre la présentation orale et la publication écrite, quelques mois plus tard, dans les Annales des Sciences naturelles (14) (les Comptes Rendus de l'Académie des sciences ne seront fondés par Arago qu'en 1835), le nombre de directions passe à 9, pour atteindre 12 dans la traduction française du Manuel de Géologie de De la Bèche (17). Vient ensuite la célèbre Notice… (8), présentée en deux temps. Charles-Henry Dessalines d'Orbigny (1806-1876), le frère cadet du grand paléontologiste, a entrepris la publication d'un monumental Dictionnaire universel d'Histoire naturelle, dont le premier volume paraît en 1841 (18). Il a demandé à Élie de Beaumont de rédiger un article sur les chaînes de montagnes. Or, celui-ci poursuit en même temps ses recherches et découvre sans arrêt de nouveaux systèmes ; il remet sans cesse la livraison de sa note, d'autant plus qu'il est alors absorbé par la rédaction du second volume de l'Explication de la carte géologique de la France (Notice… (8), Avertissement). Lorsqu'il entreprit la rédaction de l'article, le Dictionnaire en était déjà à la lettre S et, devant la lenteur de la rédaction, Charles d'Orbigny ne peut plus attendre. En 1849, il annonce à Élie de Beaumont qu'il lui a attribué 150 pages (pour un seul article, ce n'est pas si mal !) et qu'il va ainsi pouvoir composer le reste de l'ouvrage. Celui-ci paraît la même année, avec l'article sur les chaînes de montagnes qui va des pages 167 à 312 du douzième et dernier volume du Dictionnaire. Il s'arrête au paragraphe relatif au système du Sancerrois, qui porte le numéro (XVII).

Mais Élie de Beaumont a encore beaucoup à dire. Il trouve un éditeur (P. Bertrand), qui accepte de publier l'intégralité de l'article, mais dans un petit format. En fait, dès le début, il avait prévu une édition à part de son article et, dans ce but, avait fait établir sa composition typographique. C'est ce qui explique le format particulier de la notice, dont la taille des pages est proportionnée à la largeur d'une seule colonne de texte du Dictionnaire. C'est aussi la raison pour laquelle la comparaison du nombre de pages de l'article du Dictionnaire et de la Notice n'est pas très significative, sauf à préciser le nombre de signes par page. La Notice paraît en 1852, contenant l'intégralité du texte (inchangé) de l'article du Dictionnaire, qui tient cette fois en 529 pages, plus ce qui a été rédigé après 1849. Au total trois volumes, comptant 1543 pages et … 5 figures (!). Élie de Beaumont a alors identifié 21 systèmes en Europe, mais, jusqu'à sa mort, il ne cessera d'en trouver de nouveaux (Fig. 4). Dans la publication qui complète la Notice, le Rapport sur les progrès de la Stratigraphie (19), 33 nouveaux systèmes sont définis, ce qui fait au total 56. Mais, à côté de ces chiffres " officiels ", beaucoup d'autres systèmes sont en attente de vérification : Alfred Potier (13) indique qu'Élie de Beaumont lui avait déclaré en avoir inventorié 96 en 1867 et que la liste était loin d'être close.


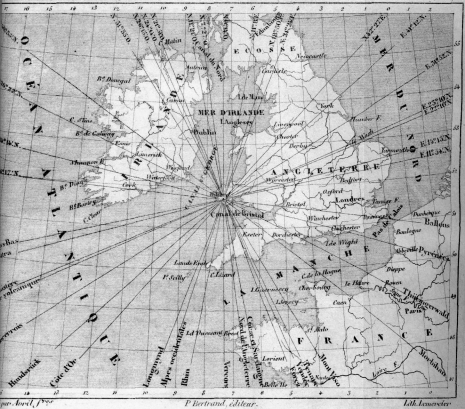
Fig. 4. " Direction des systèmes de montagnes, rapportés à Milford " (Élie de Beaumont, Notice…).

Admirateurs et adversaires

L'omniprésence d'Élie de Beaumont sur la scène universitaire, le soutien appuyé de quelques célébrités, tels qu'Arago et Alexandre von Humboldt, le plus français des auteurs allemands, font que ses idées sont rapidement acceptées, y compris par le grand public, grâce notamment aux cours publics qui fleurissent à cette époque. Il n'est pas de carte un peu générale qui ne mentionne quelques directions de systèmes, repris le plus souvent des planches 1 à 3 de la Notice. Toutefois, quelques auteurs ont un peu de mal à s'y reconnaître. Dans un des ouvrages d'enseignement les plus célèbres du XIXe siècle, François-Sulpice Beudant (1787-1850) simplifie : il mentionne treize systèmes sur le territoire français, " d'après la carte dessinée spécialement pour cet ouvrage par M. Elie de Beaumont " (20). Ces systèmes s'extrapolent à l'échelle mondiale, puisque chaque direction a une dimension planétaire. Alexandre Vézian (1821-1903), qui donne une des descriptions les plus claires et surtout les mieux illustrées de l'œuvre d'Élie de Beaumont (21), en retient en 1863 un peu moins de quarante, commençant par la Vendée pour les terrains les plus anciens (antésiluriens) et se terminant au Quaternaire par le système du Mont Ventoux, " peut-être identique à celui des Açores ". Ces deux derniers systèmes sont de son cru, ce qui montre bien qu'Élie de Beaumont a ouvert une voie de recherches qui a trouvé un large écho, dépassant le cadre de ses collègues universitaires et atteignant le grand public par l'intermédiaire des meilleurs auteurs : Stendhal dans les Mémoires d'un touriste (22), Flaubert dans Bouvard et Pécuchet :

Mais, à côté de cette popularité, des voies discordantes s'élèvent, qui vont entraîner Élie de Beaumont et ses plus proches disciples dans une sorte de " fuite en avant " pour faire triompher leurs idées. En France, l'opposition vient surtout de Constant Prévost (1787-1856), le professeur de la Sorbonne, ou de Jules Marcou (1824-1898) qui, bien que né en France, vivait principalement en Amérique où il bénéficiait d'une totale indépendance matérielle, et était donc peu sensible au pouvoir des cercles universitaires parisiens. Mais les critiques les plus vives vinrent immédiatement d'Outre-Manche, avec Sir Charles Lyell (1797-1875), dont le principe uniformitariste est naturellement aux antipodes du catastrophisme d'Élie de Beaumont. Dans le troisième volume des Principles of Geology, paru en 1833 (23), Lyell consacre au chapitre XXVII une bonne trentaine de pages pour réfuter point par point tous les arguments d'Élie de Beaumont : il n'existe aucun signe des " catastrophes " correspondant à la surrection des chaînes de montagnes, beaucoup d'extrapolations sont faites dans des régions inconnues, " jamais touchées par le marteau ", comme dit Ami Boué, un autre détracteur d'Élie de Beaumont, des montagnes de même âge peuvent avoir des directions différentes, par exemple en France et en Angleterre, des montagnes d'âge différent peuvent être de même direction, etc. Tout dépendant de la poussée en profondeur des magmas, Lyell conteste aussi le principe des cratères de soulèvement pour les volcans, visant davantage cette fois Leopold von Buch qu'Élie de Beaumont. La confrontation directe sera menée sur le plus grand volcan d'Europe, l'Etna, qui sera visité à quelques années d'intervalle par les deux adversaires (22). Élie de Beaumont ne passera que quelques semaines sur le terrain, mais il en tire une publication de plusieurs centaines de pages, publiée dans le dernier volume des Mémoires pour servir à l'Explication de la Carte géologique de la France (24). Bien entendu, la Sicile n'est pas la France, mais, dans l'esprit de l'auteur, elle était un exemple nécessaire pour comprendre les mécanismes de formation des volcans inactifs, comme ceux du Massif central. Mesurant des centaines d'inclinaisons de couches, Élie de Beaumont s'attache à démontrer, par des raisonnements qui nous paraissent aujourd'hui bien spécieux, que l'Etna est bien un cratère de soulèvement (Fig. 5). À côté de quelques considérations d'ordre général, par exemple que des bâtiments antiques construits près du sommet - la Torre del Filosofo - n'ont pas été recouverts par les retombées des éruptions plus récentes, l'essentiel de sa démonstration est basé sur l'analyse des roches éruptives. Selon lui, l'épaisseur et l'étendue des coulées successives sont incompatibles avec les pentes que l'on observe aujourd'hui. Compte tenu de la fluidité des magmas, il devrait y avoir un bourrelet à la base des coulées, qui n'est jamais observé. Les laves se sont donc déposées sur des surfaces sub-horizontales, redressées ensuite par le phénomène de soulèvement.


Fig. 5. Coupe de l'Etna dans l'hypothèse des cratères de soulèvement, d'après A. Vezian (21).

Que ce soit au sujet des volcans ou des chaînes de montagnes, Élie de Beaumont fait front, répondant point par point à toutes les critiques. Même si le noyau de ses plus fidèles adeptes s'étiole progressivement au fil des ans, il restera obstinément ancré dans ses certitudes, passant des heures à compulser des cartes et à tracer des alignements dans le secret d'un cabinet de travail où, en dépit de ses multiples fonctions, il se confinera de plus en plus pendant les dernières années de sa vie. Il pense en effet avoir trouvé la preuve irréfutable de la validité de tout son système dans un modèle théorique, le réseau pentagonal, dont il mène l'analyse en même temps qu'il poursuit les observations de terrain. La coïncidence entre les deux approches, pense-t-il, finira par faire éclater la vérité au grand jour, imposant du même coup silence à ses détracteurs.

La preuve par les mathématiques

L'analyse d'Élie de Beaumont repose sur deux ensembles de données, dont il souligne sans cesse la complète indépendance. Tout d'abord, les directions des chaînes de montagnes, qu'il a si patiemment relevées sur le terrain, ne lui semblent pas disposées de façon aléatoire. Après avoir calculé les 210 angles que forment entre elles les directions des 21 systèmes de l'Europe occidentale, il constate que ces angles, " loin de se répartir uniformément dans les 90 degrés du quart de circonférence […] se groupaient autour de certains points du quadrant, laissant presque vides les espaces intermédiaires ". Elles font donc " partie d'un réseau assujetti à un certain principe de symétrie " (19, p. 36), qu'il va chercher à identifier. Chaque chaîne, formée à un moment précis - et unique - de l'échelle des temps géologiques, a une direction donnée, qui ne se répètera plus par la suite. L'ensemble de ces directions, qui ont donc une signification chronologique bien précise, doivent se répartir de façon homogène sur toute la surface de la sphère. C'est là qu'intervient l'intuition mathématique d'Élie de Beaumont qui, procédant par essais successifs, va chercher la meilleure disposition possible. Il obtiendra ainsi un ensemble de grands cercles, définissant autant de directions qu'il fera ensuite coïncider avec celles des chaînes de montagne. Observation naturaliste et analyse mathématiques sont menées de façon totalement indépendante ; c'est une adéquation finale qui, non seulement justifiera les hypothèses de départ, mais aussi démontrera l'exactitude de tout le raisonnement.

Bien entendu, on sait maintenant que les chances de réussite étaient nulles, non seulement parce que les hypothèses de départ (refroidissement séculaire du Globe, mince croûte rigide reposant sur un noyau liquide) étaient fausses, mais aussi parce que les mathématiques rationnelles, qui étaient, dans l'esprit d'Auguste Comte, la première des sciences, ne peuvent guère s'appliquer à la complexité des phénomènes naturels. Au XIXe siècle, il en allait tout autrement. Après tout, si Laplace et Kepler l'avaient démontré pour les planètes, René-Just Haüy pour les cristaux, pourquoi ne pas chercher des lois rationnelles pour l'édification des chaînes de montagnes ?

Fort d'une culture mathématique héritée de Polytechnique, vivement encouragé par Arago qui, à l'issue de sa première présentation orale devant l'Académie des sciences, s'était exclamé que " aujourd'huy […] la Géologie a pris rang parmi les sciences exactes " (16), Élie de Beaumont se met au travail. Il commence par découper la surface de la sphère en huit triangles sphériques, par trois grands cercles, dits primitifs, passant respectivement par l'équateur et par les pôles, suivant deux directions perpendiculaires. Les sommets de ces huit triangles, groupés 4 à 4, coïncident avec ceux d'un octaèdre régulier inscrit dans la sphère, dont les arêtes sont les cordes des côtés des triangles sphériques. Ce mode de découpage, dit " octaédrique ", est complété par une série de grands cercles coordonnés aux primitifs, incluant les apothèmes des divers triangles sphériques (apothème : perpendiculaire menée du centre d'un triangle sur les côtés). On obtient ainsi un réseau de 27 grands cercles, mais Élie de Beaumont ne constate aucune coïncidence entre les directions ainsi définies et celles qu'il a observées pour les différents systèmes de chaînes de montagnes.

Il abandonne ce modèle et, poursuivant son analyse, cherche un autre mode de découpage . Il n'existe en fait que deux façons de découper une sphère par des triangles équilatéraux égaux, couvrant sans discontinuité toute la surface. Dans le plan, il n'en existe qu'un, les triangles équilatéraux, dont l'angle vaut 60°, étant assemblés par six autour d'un point. Cette disposition est impossible sur la sphère : en raison de " l' excès sphérique ", l'angle d'un triangle équilatéral sphérique sera toujours supérieur à 60°, donc l'angle couvert par six triangles adjacents supérieur à 360°, ce qui est impossible. En revanche, 360° est divisible par 4 (90°) ou 5 (72°), ce qui autorise la juxtaposition de triangles possédant ces valeurs angulaires. La première valeur (90°) correspond au système octaédrique défini ci-dessus, ou au système tétraédrique, qui en dérive directement en divisant par deux le nombre de triangles (4 au lieu de 8 - les cristallographes appelleraient cette opération une mériédrie) et qui n'apporte donc rien de plus.

La seconde valeur angulaire (72°) permet de grouper 5 triangles égaux autour d'un point. Vingt de ces triangles, groupés cinq par cinq autour de 12 points, couvrent sans discontinuité l'intégralité de la surface de la sphère. Les grands cercles correspondant aux côtés des triangles sphériques, au nombre de 15, sont dits " primitifs ". Le polyèdre inscrit dans la sphère à partir des 12 sommets est un dodécaèdre pentagonal, d'où le nom de réseau pentagonal donné par Élie de Beaumont à ce mode de découpage. Comme dans le cas du réseau octaédrique, le réseau pentagonal est complété par des grands cercles coordonnés, nommés en fonction des polyèdres inscrits et définis à partir des éléments géométriques des faces du dodécaèdre pentagonal primitif : six " grands cercles dodécaédriques réguliers ", obtenus en joignant les milieux de deux arêtes adjacentes, trente " grands cercles dodécaédriques rhomboïdaux ", joignant les sommets deux par deux, dix " grands cercles icosaédriques ou octaédriques ", joignant les milieux de deux arêtes opposées. Au total 61 grands cercles principaux, auxquels s'ajoutent un nombre plus ou moins bien défini de cercles auxiliaires, dérivant des cercles principaux par des considérations géométriques complexes. Élie de Beaumont justifie la complexité de son système par des arguments qui montrent bien l'inspiration cristallographique de ses recherches : " la stratigraphie ne peut pas plus s'arrêter [aux 61 grands cercles principaux] que la cristallographie ne s'arrête aux faces du cube, de l'octaèdre et du dodécaèdre pentagonal " (19, p. 44). Une notation spécifique est développée, avec des points principaux de premier ordre, en lettres capitales (D, I, H, T) et des points principaux d'ordre secondaire (lettres minuscules, a,b,c), le tout agrémenté d'exposants (','', etc.) pour identifier les différents pentagones.


Fig. 6. Projection sur un plan des éléments géométriques du réseau pentagonal, rapportés à un pentagone primitif (21, t. II, p. 508).


Fig. 7. Le pentagone européen, par Élie de Beaumont (8) et (19).

Toute cette analyse est extraordinairement difficile à suivre, d'autant qu'Élie de Beaumont et la plupart de ses contemporains, s'ils n'hésitaient pas à rédiger des centaines de pages, n'utilisaient guère de figures. De fait, il n'est pas facile de représenter en plan des figures de géométrie sphérique. Parmi les nombreux travaux de cette époque qui traitent du réseau pentagonal, nous n'avons trouvé qu'une figure explicitant clairement la construction des divers éléments, par Alexandre Vézian (21, vol. 2, p. 508) (Fig. 6). Encore ne s'agit-il que des cercles principaux, ne donnant pas l'illustration des cercles auxiliaires qui, dans l'esprit d'Élie de Beaumont, jouent pourtant un rôle considérable. La figure du pentagone européen donnée dans les deux ouvrages d'Élie de Beaumont (la Notice… et le Rapport sur les progrès de la stratigraphie) (Fig. 7), dont on précise plus loin (p. 145) la manière dont il a été élaboré, indique également la nature et la notation des principaux éléments du réseau, sur l'exemple concret de cette portion de la surface du Globe.

La preuve par les globes

Les représentations planes étant inadaptées à la représentation d'un espace sphérique, il faut passer par une étape indispensable, la réalisation de globes. On était justement en pleine époque de découverte du monde, avec notamment les grands voyages d'Alexandre von Humboldt et de quelques autres grands explorateurs, qui avaient entraîné, notamment en Allemagne et Tchécoslovaquie, une floraison d'ateliers confectionnant des globes topographiques de qualité. Élie de Beaumont donne ses instructions à son fidèle disciple de l'École des mines, Béguyer de Chancourtois, qui, dans le cadre de ses fonctions de professeur de topographie, va effectuer un travail considérable (2). Il fait réaliser toute une série de globes, correspondant à deux catégories :

1) La première concerne des globes de travail, sur lesquels sont représentés les éléments géométriques du réseau pentagonal. Deux exemplaires, " construits en carton et recouverts d'une sorte de stuc ", réalisés par M. Gosselin et son successeur, M. Bertaux, dans un atelier de la rue Serpente, sont conservés à l'École des mines. Tous deux sont à l'échelle du 1/100 000 000, avec un rayon de 0,037 m, une longueur de circonférence de 0,4 m, soit une longueur de grade de 0,001 m. La division centésimale des angles est caractéristique de Béguyer de Chancourtois qui, ne cessant d'explorer des voies nouvelles, s'était fait le plus ardent défenseur de l'extension du système métrique aux mesures d'angles et même de temps (25).


Fig. 8. Globe en stuc de l'École des mines, avec l'indication des principaux cercles du réseau pentagonal (détail).

Un globe, qui a beaucoup servi, porte la trace de nombreux arcs de cercles tracés au crayon, plus ou moins effacés à la gomme. Sur l'autre, en meilleur état de conservation, on distingue nettement quelques éléments du réseau pentagonal, avec l'indication des lettres caractéristiques (D, H, I, T), et la différenciation des cercles principaux par des couleurs caractéristiques (noir =primitifs, rouge = dodécaédriques, jaune = octaédriques) (Fig. 8). On a aussi matérialisé en teinte sombre quelques-uns des trente secteurs triangulaires qui ont servi au découpage initial de la sphère.

2) Un autre globe, à l'échelle du 1/50 000 000, donc d'un diamètre double du précédent (0,2548 m), comporte une carte géographique indiquant le relief des continents et océans, ainsi qu'un réseau de fils noirs et jaunes matérialisant les éléments principaux du réseau pentagonal. Beaucoup de fils jaunes (plus fins) sont malheureusement rompus, mais les fils noirs dessinent encore clairement le réseau primitif (Fig. 9). Ce globe est d'une finition plus achevée que les précédents, avec un socle en laiton qui empêche tout glissement des fils.


Fig. 9. Globe avec fond topographique (École des mines), dans lequel les directions théoriques du réseau sont indiquées par des fils et aiguilles.

D'autres globes ont été confectionnés, dont un seul a été conservé : le grand globe du Collège de France, de plus d'un mètre de diamètre, qui fut la réalisation de prestige du maître, mais qui ne semble pas avoir été beaucoup utilisé (26). Un autre globe au 1/40 000 000, d'une circonférence d'un mètre, dessiné par M. E. Picart (le dessinateur du Service géologique de l'Agence des mines, dont Béguyer de Chancourtois était le sous-directeur), a été réalisé par M. Andriveau-Goujon, 21, rue du Bac (25). Ce globe, " dont le dessin géographique est tout à fait supérieur ", semble dater de 1865, car il était destiné à l'Exposition universelle de 1867. Il a sans doute été présenté lors d'autres expositions, notamment celle de 1878, mais toujours sous la responsabilité du constructeur qui, entre-temps, le gardait dans son atelier, comme une sorte de matériel publicitaire et preuve de son savoir-faire.

Dans le Rapport sur les progrès de la stratigraphie, Élie de Beaumont conseille à ses lecteurs (19, p. 39) " d'avoir sous les yeux le globe terrestre sur lequel M. Laugel a tracé [...] le réseau pentagonal ". Il s'en explique p. 65-66 :

" Beaucoup de lecteurs [de la Notice] avaient trouvé qu'un globe avec le réseau pentagonal tracé […] sur sa surface, leur serait presque aussi nécessaire pour lire le livre qu'il ne l'avait été pour le composer.

" M. Auguste Laugel voulut bien se charger de combler cette lacune. En se chargeant des chiffres que M. Elie de Beaumont avait calculés et qu'il possédait déjà en grand nombre, il traça et fit graver le réseau pentagonal sur un globe de M. Ch. Dieu, de 30 centimètres de diamètre […]. Le globe parut, à la fin de l'année 1855, chez M. Sauret-Andriveau, géographe-éditeur, et chez M. P. Bertrand, libraire, éditeur de la Notice sur les systèmes de montagnes […]. Ce globe est beaucoup plus commode que ceux sur lesquels le réseau pentagonal a été figuré par des fils tendus [cf. globe de l'École des mines], et il met en évidence les rapports entre le réseau pentagonal et les configurations orographiques et géographiques avec une précision qui n'a d'autres limites que la petitesse de l'échelle ".

Auguste Laugel a fait don d'un de ces globes à la Société géologique de France le 14 janvier 1856 (27). Nous n'avons pu en retrouver la trace (P. Grandchamp, communication personnelle).

J'avais raison !

Alors que tout cet arsenal, qui représente une somme de travail considérable, se met progressivement en place, il reste à procéder à la démonstration finale : prouver la coïncidence des directions théoriques du réseau et celles des chaînes de montagnes. Les adversaires d'Élie de Beaumont, qui se sont surtout exprimés, en France, après la mort de celui-ci, ont eu beau jeu de dire qu'il y avait tellement de lignes dans le réseau qu'on pouvait toujours les faire coïncider avec n'importe quelle direction. Élie de Beaumont procède d'une façon qui lui semble plus rationnelle : " J'ai pensé que si les 15 grands cercles primitifs du réseau pentagonal représentaient ce qu'on pourrait appeler la forme primitive de la configuration extérieure du globe, il suffirait de placer sur un globe terrestre le réseau formé par ces 15 cercles pour rendre possible à la vue de rencontrer la position dans laquelle il devrait être placé pour se trouver en harmonie avec l'ensemble des configurations géographiques ; que, si une pareille position existait, mon œil devait finir à la saisir, et que si en effet il la saisissait, le principe même de mon travail serait sanctionné ipso facto, et la possibilité de son accomplissement assurée. En conséquence, j'ai placé sur un globe de 50 centimètres de diamètre un filet mobile composé en principe de vingt mailles ayant chacune la forme d'un triangle équilatéral de la grandeur voulue pour que le filet s'applique exactement sur la surface sphérique et l'embrasse avec une rigoureuse précision […]. Quelques tâtonnements préliminaires m'ont conduit à installer tout simplement le réseau sur le triangle tri-rectangle dont j'ai souvent parlé dans mes leçons à l'Ecole des mines et au Collège de France. Il est formé, ainsi qu'on l'a déjà vu, par les grands cercles de comparaison des systèmes de Tenare, des Alpes principales et de la grande traînée volcanique des Andes et du Japon " (Notice… (8), p. 1014-1016).

Ce " triangle tri-rectangle " n'est pas quelconque : au moment où Élie de Beaumont procédait à sa démonstration, il correspondait en effet aux systèmes les plus récents qu'il avait alors identifiés. Il est intéressant de noter qu'un seul de ces systèmes est véritablement caractérisé par des montagnes : le système des Alpes principales, où se trouvent les sommets les plus élevés, donc les montagnes les plus jeunes. Les deux autres systèmes sont en fait des axes volcaniques, ce qui montre bien, dans l'esprit d'Élie de Beaumont, l'analogie profonde entre volcans et chaînes de montagnes : " Le système du Tenare, nommé d'après le cap le plus méridional du Péloponnèse (Grèce), correspond à une étroite bande où se trouvent huit grands cercles, joignant l'Etna et des volcans, actifs ou récents, situés dans les endroits les plus divers : le Sud de l'Italie, mais aussi les îles Sandwich, l'Alaska [alors appelée " l'Amérique russe "], la pointe Sud-Est de l'Afrique, etc ". Le grand cercle de comparaison, défini par la ligne Etna-Mouna Roa, dans les îles Sandwich " marque la direction de la zone étroite où se trouvent compris l'Etna, le Stromboli, Vulcano et le Vésuve. Il est plus ou moins parallèle au plus grand diamètre de la base totale de l'Etna et à la plus grande longueur du Piano del Lago, à la direction générale de la vallée du Tibre [...] à la zone thermale de Toscane […] ; enfin, à la bande d'évents volcaniques modernes, quoique aujourd'hui éteints, qui s'observent en Sardaigne " [d'après la Notice, citée par Vézian, (21) tome 2, p. 509]. Enfin, la " grande traînée volcanique des Andes et du Japon ", qui intègre ce que l'on nommerait aujourd'hui la ceinture de feu du Pacifique, peut aussi se définir à partir de l'Etna, par une construction géométrique dont Alexandre Vézian, toujours lui, souligne comme à plaisir la complexité (21, tome 2, p. 510) : D'abord un grand cercle, " mené par le sommet de l'Etna normalement au système du Tenare ", qui représente " l'axe volcanique méditerranéen " (incluant, notamment, le pic de Ténériffe, que Leopold von Buch considérait comme l'exemple le plus typique du soulèvement). " Prolongé vers l'Ouest, il rencontre la chaîne des Andes dans la région de Cuzco […]. Si, par un point placé sur ce grand cercle à 90° du sommet de l'Etna, nous faisons passer un grand cercle qui lui soit perpendiculaire, ce nouveau grand cercle coïncidera, aussi bien que possible, avec l'axe de la bande volcanique qui, en rencontrant les îles Aléoutiennes, s'étend de la Bolivie aux îles de la Sonde. Il représente le système des Andes de M. Elie de Beaumont " (21, t. 2, p. 510).

Ces citations, que l'on pourrait multiplier à plaisir, montrent qu'Élie de Beaumont, entraînant tous ceux qui l'ont suivi plus ou moins aveuglément, quitte progressivement le monde réel pour rentrer dans un univers géométrique qui, bientôt, lui fera perdre le contact avec la réalité. Elles soulignent surtout l'importance extraordinaire qu'il a attachée à l'Etna, qui intervient dans toutes les étapes de son raisonnement. À partir de ce plus grand volcan d'Europe, le plus proche des grandes catastrophes du passé, il pensait avoir démontré, contre toute évidence immédiate, la réalité du soulèvement. Tout le reste devait donc être vrai, même si, de plus en plus, il fallait aller au-delà des apparences. Curieuse démarche d'un grand esprit qui devient prisonnier de son monde virtuel, au point de refuser toute remise en question et analyse critique.

Les adversaires d'Élie de Beaumont ont eu beau jeu de souligner que l'enchevêtrement des lignes du réseau pentagonal, avec les 61 cercles principaux et les quelques dizaines de cercles auxiliaires, était tel qu'il était toujours possible de trouver quelque coïncidence entre deux systèmes trirectangles. Mais, là encore, il était persuadé que ce réseau devait exister et, comme il le dit dans sa Notice (repris par Vézian, 21, t. 1, p. 258) " la symétrie pentagonale étant, comme principe de division d'une enveloppe sphérique, le nec plus ultra de la régularité, on pourrait ne pas lui chercher d'autre raison d'être que cette régularité même ". Il ne s'agit donc pas de trouver une, mais la coïncidence, qui apparaît d'autant plus vraisemblable que le triangle des cercles de comparaisons des trois systèmes de référence (Tenare, Alpes principales, Andes) s'applique parfaitement sur trois cercles principaux du réseau. Une fois le calage établi, tout s'enchaîne, et Élie de Beaumont n'y reviendra plus. On peut alors matérialiser l'ensemble du réseau sur des globes, d'abord par des systèmes de fils tendus sur des aiguilles comme dans l'exemplaire de l'École des mines (Fig. 9), puis par des lignes gravées sur le fond topographique, comme pour celui qui a été construit par A. Laugel ou, surtout, celui conservé au Collège de France.

Les globes n'étaient pas seulement destinés à illustrer les principes du réseau pentagonal. Ils représentaient aussi un intermédiaire indispensable pour élaborer des cartes, beaucoup plus faciles à manipuler que les représentations en trois dimensions. C'est pour cette raison que les globes réalisés par Béguyer de Chancourtois ont des échelles bien précises (1/50 000 000, 1/100 000 000), directement utilisables pour la réalisation de cartes. Le mode de projection est gnomonique, correspondant simplement à la projection à partir du centre sur un plan tangent à la sphère (Fig. 10). Pour réaliser une carte, il suffit donc de mesurer les longueurs sur le globe, grâce aux instruments de topographie sphérique conçus par Béguyer de Chancourtois, et de les reporter sur un plan tangent de référence, défini d'après la nature du polygone inscrit ou circonscrit à la sphère (octaédrique, dodécaédrique, etc.). Ce mode de projection a le grand avantage de conserver les directions, ce qui, dans l'esprit de leurs auteurs, devait permettre d'apporter la preuve définitive de la coïncidence entre les directions du réseau pentagonal et des systèmes de montagnes. Mais, grave inconvénient, l'échelle de la carte n'est pas constante, les distances variant en fonction de l'angle de projection. Il est donc plus facile de ne considérer que des surfaces relativement restreintes, ce à quoi s'attache d'abord Élie de Beaumont. Après avoir installé le réseau à partir des trois directions de référence, il s'intéresse tout naturellement au " pentagone européen ", dont le centre tombe " un peu au midi d'Erfurt, vers Remda " (8, p. 1051). Peut-être a-t-il vu un signe du destin dans le fait que ce centre de l'Europe, qui fait aujourd'hui partie de la Thuringe, n'était qu'à une centaine de kilomètres à l'ouest de Freiberg. Peut-être cela lui a-t-il rappelé le souvenir de Werner, qui restait très vivace à l'École des mines. Toujours est-il qu'il utilise le " méridien de Remda " pour caler le réseau au niveau de l'Europe, pour la " carte d'Europe en projection gnomonique sur l'horizon du centre européen " (Fig. 7).


Fig. 10. Globe de Béguyer de Chancourtois (École des mines), illustrant le principe de la projection gnomonique sur divers plans tangents à la sphère.

Grandeur et décadence

Peut-être Élie de Beaumont a-t-il eu quelques doutes en couchant sur le papier les centaines de pages de la Notice…, mais, chaque fois, la découverte de nouveaux systèmes le conforte dans ses certitudes. Il a entièrement confié au fidèle Béguyer de Chancourtois le service de la Carte géologique, lui demandant de mener à bien cette phase essentielle de sa démonstration. Celui-ci, à l'activité débordante mais confuse, développe des concepts si compliqués qu'ils en deviennent inutilisables. Son travail se poursuit dans deux directions. Tout d'abord, utilisant les instruments de trigonométrie sphérique qu'il a développés, il doit faire réaliser des cartes gnomoniques à l'échelle du Globe, qui complèteront la carte européenne de la Notice... On est alors au faîte de la puissance du Second Empire, avec les premières expositions universelles qui, à Paris, vont se tenir en 1855, puis en 1867. Les professeurs de l'École des mines y jouent un grand rôle, notamment Frédéric Le Play, lui aussi secondé par Béguyer de Chancourtois. Ce dernier en profite pour accumuler comme à plaisir médailles et titres honorifiques, mais aussi pour réaliser et exposer quelques objets qui illustrent ses travaux. C'est le cas, notamment, du dernier globe conservé à l'École des mines, donnant le principe de la projection gnomonique sur divers plans tangents à la sphère (Fig. 10). Mais les cartes se font attendre. Une seule feuille de la Carte du globe dressée en projection gnomonique sur les 8 faces sera publiée (Feuille 1B, exécutée sous la direction de M. A. E . Béguyer de Chancourtois, dessinée par M. E. Picart à l'aide des calculs faits par M. Julien Thoulet (1869-1873) (légende de l'exemplaire conservé à la bibliothèque de l'École des mines). Elle ne paraîtra qu'en 1873, un an avant la disparition d'Élie de Beaumont. La mort du dessinateur, qui semble avoir joué un rôle majeur dans toutes les réalisations graphiques effectuées à l'École des mines, donne un coup d'arrêt à ce grand projet, avant même que l'on ait pu représenter les directions des principaux systèmes de montagnes sur le fond topographique.

L'autre tâche qui avait été confiée à Béguyer de Chancourtois concernait le programme de couverture détaillée de la France au 1/80 000, décidé par l'administration des mines en janvier 1868. À cette occasion, un nouveau service fut créé, dont Élie de Beaumont fut naturellement nommé directeur. Bien entendu, celui-ci prit de Chancourtois comme sous-directeur, lui laissant toute latitude pour organiser un travail qui ne l'intéressait plus guère. Pour quelqu'un qui pensait à l'échelle du monde, la France était devenue trop petite. De Chancourtois en profita pour donner libre cours à son imagination, imaginant un système d'une extraordinaire complexité : " passer, à l'aide d'une série de transitions graduées, comportant une abstraction croissante, des faits matériels de la Géologie aux spéculations de la Science. La succession des terrains et des roches, qui constitue ces faits matériels, devait être représentée par une série appropriée de perspectives photographiques, qu'une construction géométrique transformait en coupes verticales; celle-ci servait de base à l'échelle géologique des terrains. Les cartes, les coupes et les sections longitudinales, auxquelles cette échelle était appliquée, comportaient tout un système de notations donnant, pour chaque terrain comme pour chaque roche, les variations de composition chimique, de texture physique et d'allure topographique que ces groupes présentent dans les diverses localités où ils affleurent. Enfin, l'emplacement des lieux d'extraction des matières utiles, elles-mêmes définies par un système complet de signes conventionnels, était minutieusement reporté sur les Cartes ; une Notice explicative et des légendes détaillées complétaient chaque Carte, comme chaque section, dont elles formaient des annexes " (13). Les résultats furent loin d'être à la hauteur des espérances : " A la mort d'Elie de Beaumont, en 1874, au bout de six ans, 16 feuilles avaient été livrées à l'impression, soit 3 en moyenne par année. Le travail allait trop lentement, et il avait reçu de de Chancourtois un caractère de personnalité spéculative plus marqué que ne le comportent de pareilles œuvres " (6). Quelques mois à peine après la disparition du maître, un décret réorganise le Service, avec un nouveau directeur. Oubliant réseau pentagonal et toute spéculation sur les causes, ce dernier, André-Eugène Jacquot, trouve un nouveau rythme, couvrant en peu d'années une bonne partie du territoire national. Sur le fond topographique de la carte d'état-major, les cartes au 1/80 000, dans lesquelles des générations d'étudiants ont appris les rudiments de l'analyse structurale, ne seront peu à peu remplacées par des cartes plus détaillées (au 1/50 000) que dans la seconde moitié du XXe siècle.

Ces dernières tribulations sonnent le glas d'un édifice déjà bien ébranlé. Les évènements tragiques de 1870 furent durement ressentis à l'École des mines, bombardée sans discontinuer pendant vingt jours en janvier 1871 (6). Ce n'est qu'en 1872 que les cours reprennent à peu près normalement. Depuis quelques années, Élie de Beaumont ne quittait plus guère son bureau, où venaient parfois le rejoindre ses derniers fidèles. Béguyer de Chancourtois, bien sûr, accompagné de son élève, puis adjoint pour la garde des collections, Edmond Fuchs (1837-1889). Ce dernier, qui occupera la première chaire de géologie minière à l'École en 1879, maintient une tradition qui remonte maintenant à près d'un demi-siècle : élève de Polytechnique, puis de l'École des mines, chargé des cours préparatoires, puis de topographie et, enfin, assistant de Béguyer de Chancourtois comme celui-ci l'avait été d'Élie de Beaumont. La mort d'Élie de Beaumont, qui intervient brutalement dans son château de Canon le 18 septembre 1874, laisse les deux hommes bien désemparés. Certes, il y aura de nombreuses notices dithyrambiques, des honneurs posthumes comme l'érection d'une statue à Caen, en 1876, mais le vent a définitivement tourné. Béguyer de Chancourtois, enfin professeur titulaire en 1875, a encore dix ans à vivre, pendant lesquels il continuera, de plus en plus esseulé, à défendre le réseau. En 1886, son successeur, Marcel Bertrand (1847-1907) est l'homme des nappes de charriages, apparemment aux antipodes de la pensée d'Élie de Beaumont. Comme tous ses prédécesseurs, c'était aussi un ancien élève de l'École, qui avait fait ses études au moment où le réseau pentagonal était à son apogée. Les lignes célèbres que Pierre Termier (1859-1930) a consacrées à cet épisode n'ont pas peu fait pour discréditer celui qui avait régné en maître absolu pendant tant d'années : " De 1869 à 1872, il avait suivi, sans enthousiasme aucun et même avec un dédain mal dissimulé, les cours de l'Ecole des Mines, trouvant terriblement ennuyeuse la géologie de Béguyer de Chancourtois, s'endormant à la leçon solennelle et interminable qu'Elie de Beaumont, suppléé par Chancourtois pour tout le reste du cours, venait faire sur le refroidissement du globe… " (28). Au Collège de France, la situation n'est guère meilleure. Après le bref passage de Charles Sainte-Claire Deville, les successeurs d'Élie de Beaumont, Ferdinand Fouqué puis Auguste Michel-Lévy, sont des pétrographes, plus préoccupés de la théorie du microscope polarisant que de l'orientation des chaînes de montagnes. Le premier structuraliste sera Paul Fallot (1889-1960) qui, lors de sa leçon inaugurale, prononcera certes un éloge marqué de son lointain prédécesseur (29). Mais on est alors en 1937, à la veille de la Seconde Guerre mondiale et il y a bien longtemps qu'on ne parlait plus que du géosynclinal. Pas un mot sur Élie de Beaumont de la part des auteurs de ce nouveau concept, les Américains James Hall (1811-1898) et James Dwight Dana (1813-1895), pas plus du reste que des pionniers de la tectonique des plaques, qui cette fois nous introduisent dans le monde actuel. Les louanges de Paul Fallot n'auront guère d'écho parmi ses collègues. Seul Albert de Lapparent (1839-1908), dans un Traité de Géologie qui restera un ouvrage de référence jusqu'au début du XXe siècle (30), rappelle inlassablement les principes du réseau pentagonal. Il faut dire que, polytechnicien et membre du Corps des mines comme ses devanciers, il avait été chargé en 1867 par Élie de Beaumont et de Chancourtois de participer au lever de la Carte géologique de la France au 1/80 000, et qu'il avait remplacé ce dernier dans les conférences internationales sur l'unification des unités de poids et de mesure. Mais il est bien isolé. À peu près rien ne rappelle bientôt ce qui avait été reçu avec tant d'enthousiasme un siècle plus tôt, comme si les géologues voulaient gommer de leur mémoire collective celui qui avait tenu pendant si longtemps le devant de la scène.

Un oubli immérité

Or, on redécouvre aujourd'hui que l'oubli, qui est intervenu si rapidement après la mort d'Élie de Beaumont, est aussi injustifié que ne l'avait été l'enthousiasme sans bornes de la plupart de ses contemporains. Certes, les montagnes ne se disposent pas en un réseau pentagonal, et ce qu'Élie de Beaumont pensait être une intuition géniale l'a conduit dans une impasse. Les mathématiques, tout au moins celles du XIXe siècle, ne sont pas la clef de notre monde, qui ne se refroidit, ni ne se contracte. Cela, on va bientôt le comprendre avec la découverte de la radioactivité, qui permet aux domaines profonds de notre planète de garder une température élevée. Mais on mettra du temps à en mesurer les conséquences, et les successeurs d'Élie de Beaumont, que ce soit Marcel Bertrand ou James Dana, continuent d'accepter l'hypothèse de la contraction comme le moteur de la formation des reliefs. Le titre de la série de notes dans lesquelles Dana, en 1873, utilise pour la première fois le nom de géosynclinal fait du reste explicitement référence à la contraction terrestre (31). Dana est plutôt le théoricien, mais James Hall, paléontologue de formation, est celui qui avait apporté les données de terrain à partir de la chaîne des Appalaches. En fait, tous deux étaient fortement marqués par la pensée d'Élie de Beaumont, comme A. M. C. Sengör l'a montré avec talent dans un livre remarquable (32). Le concept de géosynclinal repose sur l'idée d'un bassin subsident, s'approfondissant en même temps qu'il se remplit de sédiments, avant d'être le siège d'un mouvement opposé, à savoir la surrection brutale de la chaîne. Dans l'esprit d'Élie de Beaumont, ces deux phases correspondent aux fuseaux et aux bossellements, dont il décrit en grand détail les caractéristiques respectives. Concernant les bassins, le fait le plus important, correspondant au phénomène de subsidence, est l'épaississement progressif des couches sédimentaires des bords au centre du bassin. Or, c'est précisément cette structure qui est décrite par Élie de Beaumont dans de nombreuses régions (Bassin de Paris, Caucase), et Hall s'est essentiellement appliqué à la retrouver dans les Appalaches. En fait, Dana est très critique à son égard, et il a été amené à proposer le nom de géosynclinal pour s'opposer aux interprétations de Hall. Comme l'écrit A. M. C. Sengör (32, p. 123 sq.) : " Few have realized that what had become accepted as the geosynclinal theory of mountain-building was (a) Dana's interpretation of Hall's observation on sedimentary thickness changes in and around the Appalachians on the basis of Elie de Beaumont's theoretical views, and (b) the "geosynclinal theory" (as it has become known) had nothing to do with Hall except the inspiration his observations and statements gave to Dana to rehash Elie de Beaumont's ideas ". (p. 126). Autrement dit, le terme de " géosynclinal " qui, singulier pouvoir des mots, assura immédiatement à son auteur une célébrité durable, a été créé pour " réchauffer " (traduction exacte du terme " rehash ") les idées d'Élie de Beaumont. Ce dernier, qui est mort une année après la parution des articles de Dana, a dû en avoir connaissance, mais on ne connaît pas ses réactions. Comme beaucoup d'autres théories, il en sera du géosynclinal comme du réseau pentagonal. Après la Seconde Guerre mondiale, il sera balayé par la révolution de la tectonique des plaques. Gageons qu'Élie de Beaumont qui, après la découverte de la radioactivité, aurait du revoir ses conceptions du refroidissement du Globe et de la durée des phénomènes géologiques, aurait bien aimé cette nouvelle théorie qui, par le biais des collisions océaniques ou continentales, redonne un certain aspect catastrophiste à la formation des reliefs. Il y a en tout cas quelque chose qui lui aurait beaucoup plu, où l'on peut voir une survivance directe du mode de travail qu'il avait instauré : l'habitude qu'ont prise les stratigraphes, officialisée par l'échelle stratigraphique internationale de l'International Union of Geological Sciences (IUGS), de représenter dans la colonne de droite les phases orogéniques successives ayant affecté la surface du Globe. On remplace le nom de phase par celui de système (réservé maintenant par les stratigraphes aux terrains horizontaux) et on retrouve le principe qui a guidé Élie de Beaumont dans toutes ses recherches, remis cette fois à sa juste place.

Remerciements :

Lorsque, intrigué par les globes de l'École des mines, j'ai commencé de m'intéresser à Élie de Beaumont, je n'imaginais certes pas le cheminement tortueux qu'il me faudrait accomplir, pour lequel j'ai bénéficié de l'aide des services de documentation de la bibliothèque de l'École des mines (Marie-Noëlle Maisonneuve et Thierry Delettre) et des Archives de l'Académie des sciences (Claudine Pouret). Des versions successives de cet article ont bénéficié des commentaires et critiques de Jean Gaudant, Celal Sengör, Michel Durand-Delga et surtout de Philippe Grandchamp, qui m'a permis d'améliorer considérablement l'intérêt de cet article, et que je remercie très chaleureusement. Sauf pour la Figure 1 b (Archives de l'Académie des sciences), toutes les illustrations (photos de l'auteur) proviennent d'objets ou de documents conservés au musée et à la bibliothèque de l'École des mines.

Références