COMITÉ FRANÇAIS D'HISTOIRE DE LA GÉOLOGIE (COFRHIGEO) (Séance du 30 mai 1984)

Les observations de Bouguer au Chimborazo ne nous apparaissent que comme le point culminant de cette longue aventure que furent les expéditions des Académiciens au Pérou et en Laponie. Et il me paraît indispensable de retracer le cadre intellectuel dans lequel cela se place.

Ce qu'était la perception par le grand public du problème se trouve formulé par un passage d'une oeuvre de jeunesse de Diderot, "les bijoux indiscrets", publiée en 1748. Je rétablis les noms dans ce que la fiction place dans l'Académie d'un pays imaginaire :

"Elle était alors divisée en deux factions, l'une composée des Vorticoses, et l'autre des attractionistes. Descartes, habile géomètre et grand physicien, fonda la secte des vorticoses. Newton, habile physicien et géomètre fut le premier attractionnaire. Descartes et Newton se proposent l'un et l'autre d'expliquer la nature. Les principes de Descartes ont au premier coup d'oeil une simplicité qui séduit ; ils satisfont en gros aux principaux phénomènes, mais ils se démentent dans les détails. Quant à Newton, il semble partir d'une absurdité : mais il n'y a que le premier pas qui coûte. Les détails minutieux qui ruinent le système de Descartes affermissent le sien. Il suit une route obscure à l'entrée, mais qui s'éclaire à mesure qu'on avance. Celle, au contraire, de Descartes, claire à l'entrée, va toujours en s'obscurcissant..."

Les mesures des arcs de méridiens par les Académiciens ont-elles constitué l'expérience cruciale permettant de trancher le débat ? Nous allons voir que les choses ne sont pas si simples.

Il sortirait de mon sujet d'évoquer l'émergence de l'astronomie moderne : l'héliocentrisme de Copernic, la définition d'orbites non circulaires avec les trois lois de Kepler, dont nous conservons l'énoncé : les rayons balayent des aires égales dans des temps égaux - l'orbite est une ellipse dont le soleil occupe un foyer - les carrés des temps de révolution sont comme les cubes des grands axes ; l'introduction de la lunette par Galilée, avec la découverte des satellites de Jupiter (dès la première nuit d'observation !), celle des phases de Vénus, preuve de l'héliocentrisme, et celle des taches du soleil, preuve qu'il n'était pas formé d'une matière incorruptible.

Mais ce développement de l'astronomie s'accompagne de l'éclosion beaucoup plus lente et difficile d'une "philosophie naturelle", se substituant bien péniblement à l'esprit scolastique. Les résistances, qui culminent avec la condamnation de Galilée, visant bien plus la méthode de cette philosophie naturelle, que l'héliocentrisme (ou les taches du soleil).

Le livre de Copernic - dont il n'a reçu le 1er exemplaire que le jour de sa mort - comportait une préface non signée, rédigée par l'éditeur, Osiander sans l'aveu de l'auteur, qui prenait la précaution de dire que le système était un mode de calcul des apparences, et ne préjugeait pas de la réalité. Précaution oratoire prise sans doute à l'égard des Luthériens, car les plus hautes autorités de l'église étaient depuis longtemps au courant du système de Copernic, et ne paraissent pas s'en être offusquées. Mais rien ne permet d'affirmer que Copernic soit mort de rage en lisant la préface d'Osiander, comme certains ont pu le dire.

Kepler avait énoncé une autre loi, outre celles que nous avons conservées : "les rayons des orbites de deux planètes consécutives sont dans le rapport des rayons des sphères, inscrites et circonscrites à un polyèdre régulier", ce qui témoigne d'une forme de pensée qui nous est devenue bien étrangère.

Galilée soutenait encore, contre Kepler, la perfection du mouvement circulaire, et il défendait l'influence astrologique des satellites de Jupiter.

Dans l'éclosion d'une "philosophie naturelle", Descartes joue un rôle essentiel, avec sa physique, où il tente une explication à base géométrique, admettant une matière subtile dont les tourbillons échappent aux sens, mais qui produit l'attraction centripète.

C'est Huygens qui développe, dans le cadre de la dynamique Galiléenne, la théorie de la force centrifuge. Il montre que celle-ci, combinée à la force dirigée vers le centre (peu importe la manière dont Descartes l'expliquait), doit entraîner un aplatissement de la Terre, de 1/578, ceci ne dépendant que du rapport entre la force centrifuge et la pesanteur à l'équateur, dont la valeur, 1/289, était déjà connue sans ambiguité (ce rapport ne dépend que du rayon equatorial, de la durée du jour sidéral et de la longueur du pendule battant la seconde).

Le premier livre des "Principes" est consacré à ce qu'on pourrait appeler de la technique mathématique ; c'est au début du IIIème livre que Newton donne un tableau de l'univers qui fait apparaître la loi de la gravitation. Il montre que le système des satellites de Jupiter, celui des satellites de Saturne, le système des planètes autour du Soleil, de par la 3ème loi de Kepler, correspondent à des attractions en 1/r², ce qui résulte aussi de la forme elliptique des orbites, conformément à la 2ème loi de Kepler (mais beaucoup des orbites sont très proches du cercle).

Il montre ensuite - et c'est l'étape la plus célèbre de sa démonstration, que la gravité sur la Terre, avec une variation en 1/r2, correspond à la force qui retient la lune sur son orbite.

Tout cela serait vrai si les centres des astres s'attiraient mutuellement, ce dont les tourbillons de Descartes pourraient rendre compte.

Mais Newton a la hardiesse de supposer que ce sont toutes les particules de matière qui s'attirent les unes les autres. Cela n'entraîne aucune différence pour les astres éloignés.

Mais, pour une planète tournant sur elle-même, et que la force centrifuge aplatit, selon Huygens, de ce qu'elle est déformée résulte que l'attraction qu'elle produit n'est plus dirigée vers le centre.

Newton calcule pour un ellipsoide homogène, la différence entre l'attraction au pôle et à l'équateur. Il est en train de créer le calcul intégral et l'instrument mathématique est encore imparfait. Il obtient "by computation", c'est-à-dire, apparemment, par l'estimation de la surface d'une courbe, tracée point par point, un résultat que nous pouvons vérifier très rapidement. Il en résulte que : une terre homogène doit être aplatie de 1/233, et que la gravité varie du pôle à l'équateur, dans la même proportion.

Or, cette variation était connue depuis le voyage de Richer à Cayenne en 1672, car celui-ci avait dû y modifier le réglage de son horloge astronomique. Dans la 2ème édition des Principes (1713), Newton cite toute une série d'observations dans le même sens, mais postérieures à la 1ère édition (1688). Il donne une table de la longueur du pendule battant la seconde, en fonction de la latitude, calculée pour l'aplatissement indiqué ci-dessus.

Les variations de la gravité (ou de la longueur du pendule) observées sont plus fortes que ne l'indique la table ; "a little greater" écrit Newton, mais en fait, doubles en moyenne. Elles seraient compatibles avec l'aplatissement de Huygens.

Par ailleurs, on connaissait la rotation de Jupiter, qui est très rapide (10 H), le diamètre et le rapport de sa masse à celle de la Terre, l'aplatissement théorique calculé par Newton de 1/10 pour une densité uniforme (on adopte plutôt 1/11) et un aplatissement observé de 1/12 à 1/15, alors qu'il serait de 1/23 avec la théorie de Huygens. Il n'y a donc pas, alors, de données assez précises pour trancher.

On sait que Newton avait eu besoin, pour comparer la gravité et l'attraction de la lune, de connaître la rayon de la Terre. Il avait d'abord admis une valeur erronée, et comme la vérification ne se faisait pas, il avait abandonné son projet.

Puis, il a connu la triangulation de Picart, entre Paris et Amiens (1669-1671), qui lui a fourni le rayon de la Terre utilisé dans les Principes.

En fait, il y avait eu d'autres mesures d'arcs de méridien. La première triangulation est celle de Snellius (1617) entre Alcmaer et Berg Opsom, aux Pays Bas qui indique une longueur du degré de méridien de 28473 "perches du Rhin".

Riccioli, à Bologne avait déterminé le degré en "pied de Bologne" (mais il semble qu'il y avait deux pieds différents, selon les usages). Cassini, après être allé mesurer les unités respectives, a tenté d'exprimer les résultats en toises de Paris, et constaté que, pour ces trois arcs (avec celui de Picart), la longueur du degré diminuait du Sud au Nord, ce qui suggérait une Terre allongée suivant l'axe. Ceci ne s'accompagne d'aucune tentative d'interprétation physique, ni de discussion critique.

Colbert, peu avant sa mort, avait ordonné à Cassini (le premier de la dynastie), de prolonger la méridienne de Picart sur toute la longueur du royaume. La Hire fut chargé du prolongement d'Amiens à Dunkerque, tandis que Cassini poussait vers le Sud. Il avait atteint Bourges, où l'hiver de 1683 l'arrêta, et la triangulation ne fut reprise qu'en 1700 (avec l'aide de son fils), et poussée jusqu'au Canigou. On mesure une base sur la plage du Roussillon, et la latitude par des observations d'étoiles à Collioure.

Le résultat de ces mesures est que le degré moyen est plus long entre Paris et Collioure, qu'entre Paris et Dunkerque. Les Cassini sont confirmés dans leur idée d'une terre allongée, et Cassini publie en 1720 des tables, indiquant la longueur du degré de méridien (et de parallèle), en fonction de la latitude, ce qui doit aider à la navigation en permettant le calcul de la distance de deux ports.

Il y a donc là une contradiction flagrante avec la table qui avait été donnée par Newton, donnant la longueur du degré selon la latitude, calculée pour l'aplatissement de 1/233.

D'où l'idée de confirmer ou d'infirmer ces tables en mesurant un degré de méridien (la mesure d'un degré de parallèle serait techniquement plus difficile) sous l'équateur.

Ce projet a été retenu par le Ministre Maurepas (le cardinal Fleury étant premier Ministre), sans qu'on sache très bien dans quelle mesure il était mu par le souci d'aider la navigation, ou de trancher un problème, aussi philosophique que scientifique. Avec un financement assuré par l'Etat (mais qui fera problème par la suite), l'expédition des Académiciens Godin, Bouguer, La Condamine, au Pérou est organisée, et part en Mai 1735.

Parmi leurs compagnons, il faut citer Joseph de Jussieu, botaniste comme ses frères.

L'expédition arrive sur place un an plus tard, et connaîtra d'innombrables aventures, reprises dans un livre récent, "le Procès des Etoiles", par Florence Trystam, qui se lit comme un roman.

Bouguer a mesuré la gravité à diverses escales (49°, 18°, 9°, 0°) et trouve une variation un peu plus importante que celle indiquée par la table de Newton, mais il ne le remarque pas.

Le graphique ci-après indique, en fonction de la latitude, les longueurs du pendule dont l'oscillation simple est de une seconde, en pieds et lignes dont il est question ici (et qui sont toutes rapportées à la longueur à Paris).

Newton conclut : "Et donc la Terre est un peu plus haute sous l'équateur que ne l'indique la table, et un peu plus dense au centre que dans les mines près de la surface, à moins que, peut-être la chaleur de la zone torride ait un peu augmenté la longueur du pendule".

Suit une longue discussion sur la dilatation thermique, alors que la température n'a pratiquement jamais été observée.

Newton rend hommage au soin de Richer dont il écrit : "if this gentleman's observations are to be depended on, the earth is higher under the equator than at the poles, and that by an excess of about 17 miles", ce qui est la valeur qu'il a calculée. Quant aux autres valeurs citées, il en dit, se référant à Richer : "this diligence and care seems to have been wanting to the others observers". L'hypothèse de Newton intuitive, sur la Terre "un peu plus dense au centre que près de la surface" annonce la théorie de Clairaut.

Newton suppose, ailleurs, que la densité de la Terre pourrait être comprise entre 5 et 6, sans donner aucune justification, dans un passage (livre III, proposition X, théorème X), assez obscur, où il envisage l'effet de la résistance de l'air sur le mouvement des planètes.

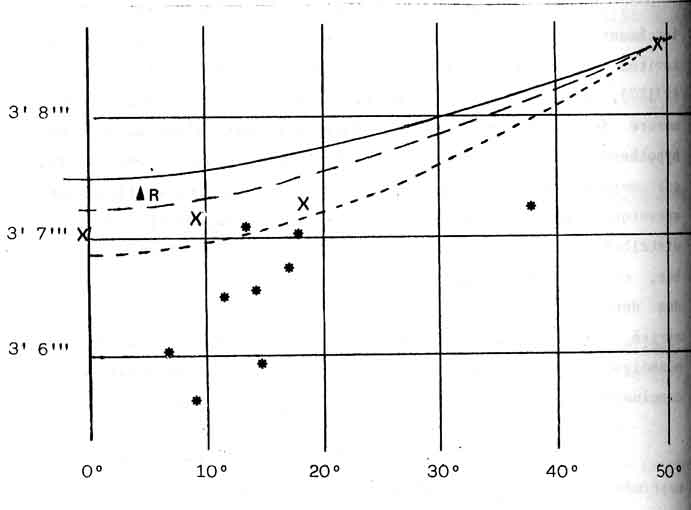
Trait plein : table calculée par Newton.
R : valeur de Richter à Cayenne.
Tirets longs : calcul à partir de la valeur internationalement admise comme référence.
Tirets courts : Calcul par la formule de Clairaut, pour l'aplatissement 1/578 de Huygens.
Croix : mesures de Bouguer.
Etoiles : valeurs citées par Newton dans la 2ème édition des Principes.

Bouguer a l'idée qu'il doit être possible de mettre en évidence l'attraction par une montagne isolée. A vrai dire, il y avait déjà pensé en Europe, mais n'avait pas trouvé de montagne isolée d'un volume suffisant. A-t-il eu une réminiscence de la lecture des Principes de Newton (dont il n'aurait pu connaître que le texte latin ?). Dans le "système du Monde", qui suit la fin des "Principes Mathématiques", au paragraphe 22, Newton explique pourquoi on n'observe pas l'attraction mutuelle de deux corps, qui est beaucoup trop faible (cette attraction ne sera mise en évidence au laboratoire que par Cavendish, en 1798, qui détermine ainsi la constante de la gravitation, et du même coup, la densité moyenne de la terre).

Et il prend comme exemple une montagne hémisphérique, haute de 3 miles (5000m), d'un diamètre à la base de 6 miles (10 km), qu'il sous-entend de même densité que la Terre, et qui ne dévierait la verticale, que de moins de 2' (en fait, 1' 21") .

Mais au Pérou, les immenses volcans qui bordent la vallée de Quito paraissent à Bouguer rendre l'expérience possible : il s'agit de mesurer la latitude d'un point situé au Sud (ou au Nord) de la montagne, le plus près possible, de jalonner une ligne Est-Ouest, et de mesurer la latitude d'un point de cette ligne éloigné de la montagne. Bouguer choisit le Chimborazo, dont il calcule le volume, ayant mesuré la hauteur et le diamètre de sa base. Il n'applique pas la formule du cône, ayant reconnu que les flancs sont concaves.

Le rapport de ce volume à celui de la Terre est très petit (1/7.400.000.000), mais il envisage une station à 1800 toises du sommet et le carré du rapport de cette distance, à celle au centre de la Terre, le conduit à prévoir une déviation de 1/2000, soit 1'43", qu'il sait pouvoir mettre en évidence par des mesures de latitude.

Il monte donc, le 4 décembre 1738, à la station prévue, à 4670m d'altitude, où il trouve des conditions épouvantables. Pour le première fois, l'officier espagnol qui lui sert d'ange gardien l'abandonne.

Il s'installe, avec La Condamine, et peut observer pendant les nuits du 14 et du 15 décembre. Puis il se rend à la station du plateau, qui n'est pas exactement à l'Ouest (W 8° S), mais la correction est facile à faire, et sûre. Il observe dans la nuit du 22 décembre, et ses calculs lui indiquent une différence de latitude de 7"1/2. C'est une profonde déception, qu'il avoue crûment dans la note qu'il envoie néanmoins à l'Académie dès le 30 décembre.

La brièveté du délai de rédaction - une semaine, sans doute sérieusement entamée par le retour à Quito - peut surprendre. Je suppose qu'il devait y avoir un départ de courrier (ce qui n'arrivait pas tous les jours) qu'il ne voulait pas manquer. Effectivement, la note parvient à l'Académie où elle sera lue l'année suivante.

Le calcul préliminaire - celui de 1'43" - était fait d'avance, et certainement rédigé. J'imagine même que la note était prête, et qu'il n'y avait plus qu'à mettre des chiffres dans les blancs. Pas un instant, Bouguer n'envisage d'abandonner l'hypothèse de l'attraction newtonienne, mais il n'a pas le temps de revoir ses calculs. Dans le désarroi de l'échec, il mentionne seulement l'explication qui lui vient à l'esprit : le Chimborazo peut être moins dense que la Terre. Il précisera, lors de la réimpression de cette note dans le volume publié à son retour "peut-être 4 à 5 fois" (nous savons depuis Cavendish, qu'il faudrait dire "2 fois", la densité moyenne de la Terre étant 5,52).

Bouguer ajoute aussi qu'il a appris, plus tard, que le Chimborazo est un volcan, ce qui signifie pour lui qu'il peut comporter des cavités intérieures.

D'où vient cet échec ? J'ai eu le privilège il y a quelques années grâce à des géologues pétroliers amis, de pouvoir disposer des cartes topographiques du Chimborazo, au 1/50 000, levées par stéréotopographie aérienne, qui avaient paru l'année précédente.

J'ai pu, sans ambiguité, y situer les deux stations de Bouguer. Il était facile d'y calculer la déviation de la verticale, par une méthode aujourd'hui classique : on applique sur la carte un calque, divisé par des cercles et des rayons, tels que chaque compartiment ait un effet proportionnel à la différence d'altitude. Et j'ai trouvé une différence de déviation de 11". Quelle était la précision des mesures de la latitude de Bouguer ?

Reprenant les angles observés, on trouve, pour chaque étoile, un écart probable de l'ordre de 8", soit pour 4 ou 5 étoiles, un écart probable de 4". Les 11" calculées sont bien dans la marge 7"1/2 + 4". Les mesures étaient bonnes (et Bouguer qui, sans disposer d'une théorie des erreurs, sentait bien la précision atteinte, savait qu'elles ne signifiaient rien).

D'où vient l'écart entre mes 11" calculées et les 1'43" (dix fois plus) trouvé par Bouguer ? Il y a d'abord un facteur 2 (et non pas 4 ou 5) pour la densité de la Terre.

Une cubature faite sur la carte indique une surestimation du volume d'ordre de 50% (mais qu'est ce que la base rapportée au plateau ?).

Mais surtout, Bouguer confond l'attraction par un cône, avec celle de sa masse rassemblée au centre de gravité (ce qui n'est vrai que pour la sphère). C'est d'autant plus surprenant qu'il est à mi-hauteur du flanc, et a donc derrière lui, agissant en sens inverse, une partie du cône. Partant des dimensions qu'il indique, je trouve que ceci entraîne une erreur dans un rapport de 4.

Par ailleurs, Bouguer a fait des mesures de g à Quito, et au sommet du Pichincha, qui domine la ville. Comparées à la mesure au niveau de la mer, les valeurs qu'il trouve sont - presque - dans le rapport des carrés des distances au centre de la Terre - ce que nous appelons la "Correction à l'air libre". Mais il veut tenir compte de l'attraction par la matière du plateau (ce que nous appelons la "Correction de Bouguer"), et le calcule correctement. Mais l'effet réel de cette attraction est très faible, ce qui ne le surprend pas, puisqu'il est prêt à admettre que la densité de ce plateau est très inférieure à celle de la Terre. Et c'est ainsi qu'il est passé à côté de la découverte de la compensation isostatique (qui n'était pas du tout mûre). Celle-ci n'explique d'ailleurs pas l'échec de Chimborazo.

Et pendant ce temps, que se passait-il en France ?

En 1736, un an après le départ de Bouguer, l'Académie envoie Clairaut et Maupertuis mesurer un arc de méridien en Laponie. Ils sont accompagnés par le physicien suédois Celsius et terminent le travail dans l'année ; ils reviennent dès la fonte des glaces en 1737. Mais leur arc ne mesure que 57'. Comparé à celui de Picart, il fait apparaître un aplatissement de 1/177, ce qui est trop.

Clairaut et Maupertuis remesurent les latitudes de Picart, vérifient sa toise (l'étalon est celui exposé en bas de l'escalier du grand Chatelet où tout le monde peut l'utiliser, de même que le mètre de la rue de Vaugirard est à la disposition de tous). Cela n'arrange rien.

Clairaut reprend la théorie mathématique de l'aplatissement dans un livre admirable, publié en 1743 (réimprimé en 1808).

Il envisage, non seulement le globe homogène, mais un globe formé de couches fluides à densités échelonnées, et il associe la variation de la gravité à l'aplatissement trouvé : la somme de la variation relative du rayon (a-b)/a, et de la gravité (g_p-g_e)/g_e ; est égale à 2,5 ω² a/g_e , deux fois et demie le rapport de la force centrifuge à la gravité à l'équateur.

L'aplatissement de 1/177 n'est pas possible pour un globe fluide. Il est incompatible avec ce qu'on sait des variations de la gravité qui sont beaucoup trop fortes. Clairaut conclut à une erreur (ou plutôt, une précision insuffisante), des mesures, et reconnaît la pré-éminence de la théorie mathématique.

Entre temps, Cassini III (dit "de Thury") publie en 1744 le résultat d'un contrôle des latitudes pour la méridienne de son père et son grand-père. Outre Paris et Dunkerque, il a mesuré les latitudes de Bourges, Rodez et Perpignan avec des instruments nouveaux, en tenant compte de l'aberration (déplacement apparent des étoiles fixes au cours de l'année, découvert par Bradley en 1727). Il a donc des mesures surabondantes. Il est clair que la longueur du degré diminue du Sud au Nord, et que la Terre est aplatie. Combinant de différentes manières les cinq arcs dont il dispose, la première valeur que donne Cassini de Thury est 1/283 très proche de la valeur 1/292 actuellement admise.

Il eût évidement été plus simple de contrôler, dès que les divergences sont apparues, la latitude de Collioure, sans avoir à aller au bout du monde.

La question était donc réglée quand Bouguer rentre en France. Il publie son Mémoire en 1749 - mais c'est sans doute ce qu'il a rédigé en Amérique. Pas une allusion à ce qui a été fait entre temps en France. Il ne connaît que la longueur (mesurée...) de l'arc de Laponie. Avec celui de Picart, et le sien, cela fait trois ; c'est surabondant pour déterminer une ellipse ; il cherche un ovale qui ne soit pas une ellipse, et propose une forme très peu vraisemblable.

Seul, Bernardin de St Pierre, à la veille de la Révolution, mettra encore en doute l'attraction newtonienne et l'aplatissement de la Terre.

Que conclure ? Il ne faut pas confondre, nous avons essayé de le montrer, une généralisation prématurée de mesures insuffisamment précises des Cassini, qui avaient acquis une apparence de légitimité par la publication de tables destinées à la navigation, avec le dilemme : Descartes ou Newton ?

La vérification de ces mesures s'imposait. Elle a un peu tardé, mais ce retard a permis la construction d'instruments nouveaux, et la prise en compte de l'aberration. Même si les Cassini, du seul fait qu'ils ne suivaient pas les Principes de Newton, apparaissaient comme des Cartésiens, la physique de Descartes n'avait rien à faire dans le modèle d'une Terre allongée.

Et, d'autre part, il y avait la question de la valeur de l'aplatissement, qui ne fournissait pas un critère pour choisir entre Newton et Descartes. L'aplatissement calculé par Huygens correspondait (il ne la savait pas), dans la théorie de Newton, à un globe avec une très forte concentration de masse au centre. Le calcul de Newton était fait pour une Terre de densité uniforme. La valeur à retenir pour l'aplatissement, qui s'est progressivement dégagée des mesures, est liée à l'échelonnement des densités avec la profondeur, intermédiaire entre les deux modèles ci-dessus. La fait que l'aplatissement soit moindre, et la variation de la gravité plus forte, que ne l'avait prévu Newton n'a jamais été retenu contre la théorie de l'attraction, même si on n'a pas tout de suite compris (à défaut de démonstration, on pouvait le sentir intuitivement) que cela dépendait de l'échelonnement des densités.

Il n'y a donc pas eu d'expérience cruciale. L'attraction newtonienne s'est imposée par la multiplicité des contrôles de ses conséquences mathématiques souvent très indirectes (marée, précession des equinoxes, perturbations des mouvements de la lune et des planètes...).

On pourrait en dire autant de la relativité. Ce n'est pas l'expérience de Michelson qui la prouve (elle écarte seulement une certaine conception de l'éther), mais ses applications, telles que le fonctionnement des accélérateurs de particules.

On peut aussi tirer de cette histoire une morale : quand un ministre, tel Maurepas se mêle de choisir lui-même l'expérience à financer, il risque fort d'être tenté par ce qui paraît sensationnel et spectaculaire et non par l'expérience réaliste et bien préparée, qui permettrait un avancement effectif des connaissances scientifiques. Peut-être l'Académie, si elle avait été libre de l'emploi des fonds, se serait-elle rendu compte que le plus simple aurait été de vérifier la latitude de Collioure (au risque de soulever des susceptibilités personnelles).

Cette morale n'a rien perdu de son actualité.

BOUGUER P. - La figure de la Terre, déterminée par les observations de MM. Bouguer et La Condamine , in 4°, Paris, Joubert 1749.

CASSINI - De la grandeur et figure de la Terre. Mémoires de l'Académie Royale des Sciences 1718. Paris 1720.

CASSINI de THURY - La Méridienne de l'Observatoire royal de Paris, vérifiée sur toute l'étendue du Royaume par de nouvelles observations pour en déduire la vraie grandeur des degrés de la Terre . Paris MDCC XLIV.

CLA1RAUT - Théorie de la figure de la Terre (1° édition, 1743), 2° édition, Paris, Courcier 1808, XL + 308p.

DALY (Reginald Aldworth) - Strength and structure of the Earth , un volume de 434 pages. New York. Prentice - Hall inc 1940.

DIDEROT (Denis) - Oeuvres , édition de la Pléiade, 1963.

GOGUEL (Jean) - Bouguer au Chimborazo . Bulletin géodésique . Nouvelle série, année 1971, numéro 101, premier septembre 1971, p. 329-334, 1971.

MAUPERTUIS - Oeuvres de M. de Maupertuis . A Dresde, chez George Conrad Walther, libraire du Roy, 1752.

NEWTON (Sir Isaac) - Mathematical Principles of Natural Philosophy and his system of the World . - Translated into English by Andrew Motte in 1729 - Révisé et publié par Florian Cajori, 1962, University of California, Press, 2 volumes.

M. François Ellenberger signale que Buffon écarte l'hypothèse de cavités intérieures dans le globe, à cause de l'étude de la gravité.

Dans cette hypothèse, la gravité serait plus faible dans les montagnes. D'autre part, il rejette comme inutile la notion de densités croissant vers le centre de la Terre et postule au contraire un globe de densité uniforme.

M. Jean Goguel pense que cela doit résulter d'une lecture, forcément superficielle, de l'ouvrage de Clairaut. En fait, des cavités intérieures auraient permis d'expliquer l'aplatissement (1/177), trop fort pour un globe homogène, qui résulte de la mesure de l'arc de Laponie. Mais Clairaut s'est donné comme hypothèse de travail un équilibre hydrostatique, c'est-à-dire, qui serait valable pour un liquide et un tel équilibre est mécaniquement incompatible (il y aurait instabilité) avec une distribution des densités qui n'irait pas en croissant vers le bas, et c'est pour cela qu'il rejette la distribution, comportant des densités faibles (ou des cavités) centrales. Buffon (et c'est arrivé bien souvent à d'autres), en face de calculs dont il n'analyse pas la démarche, confond l'hypothèse de départ et la conclusion.

M. André Cailleux ayant mentionné la position qui lui avait été exprimée aux USA, M. Goguel indique que c'est celle de Reginald Aldworth Daly, dans "Strength and Structure of the Earth", publié en 1940. Le début du chapitre II "Development of the Idea of Isostasy" présente Bouguer comme un précurseur de l'isostasie, mais à la suite d'une analyse de seconde main, qui ne doit pas prévaloir contre l'examen des textes originaux.

Le véritable précurseur de l'idée d'isostasie, formulée (sans le nom) par Airy en 1855, paraît être Sir John Herschel (le fils du découvreur d'Uranus) dont Daly cite une lettre du 20 février 1836 (voir également : Proc. Geol. Soc. London , volume 2, 1837, page 597), qui envisage une écorce mince en équilibre sur un noyau planétaire trop chaud pour cristalliser, et donc assez mobile pour s'écarter (to flow away) de secteurs nouvellement chargés de sédiments.

Il est sous-entendu que le "noyau planétaire" est en équilibre au sens de Clairaut, dont l'oeuvre est alors un classique.

Voir aussi C. Babbage : auquel était adressée la lettre de Herschel.


Mis sur le web en 2009 par R. Mahl