COMITÉ FRANÇAIS D'HISTOIRE DE LA GÉOLOGIE (COFRHIGEO) (séance du 14 mars 2001)

René-Just Haüy, initialement amateur de botanique, s'étonnait - selon Georges Cuvier - de la constance des formes des fleurs, des fruits, et ne concevait pas que les formes des minéraux, plus simples, ne fussent pas soumises à de mêmes lois. " Ce fut lorsqu'il était rempli de ces idées, qu'examinant quelques minéraux chez … M. Defrance, … il eut l'heureuse maladresse de laisser tomber un beau groupe de spath calcaire cristallisé en prismes. Un de ces prismes se brise de manière à montrer sur sa cassure des faces non moins lisses que celles du dehors, et qui présentaient l'apparence d'un cristal nouveau tout différent du prisme pour la forme. M. Haüy ramasse ce fragment ; il en examine les faces, leurs inclinaisons, leurs angles. A sa grande surprise il découvre qu'elles sont les mêmes que dans … le spath d'Islande.

" Un monde nouveau semble à l'instant s'ouvrir pour lui. Il rentre dans son cabinet, prend un spath cristallisé en pyramide hexaèdre … dent de cochon ; il essaie de le casser, et il en voit encore sortir ce … spath d'Islande ; les éclats qu'il en fait tomber sont eux mêmes de petits rhomboïdes : il casse un troisième cristal, … lenticulaire ; c'est encore un rhomboïde qui se montre dans le centre, et des rhomboïdes plus petits qui s'en détachent.

" Tout est trouvé , s'écrie-t-il ! les molécules du spath calcaire n'ont qu'une seule et même forme : c'est en se groupant diversement qu'elles composent ces cristaux dont l'extérieur si varié nous fait illusion ; et, partant de cette idée, il lui fut bien aisé d'imaginer que les couches de ces molécules s'empilant les unes sur les autres, et se rétrécissant à mesure, devaient former de nouvelles pyramides, de nouveaux polyèdres, et envelopper le premier cristal comme d'un autre cristal où le nombre et la figure des faces extérieures pourraient différer beaucoup des faces primitives, suivant que les couches nouvelles auraient diminué de tel ou tel côté, et dans telle ou telle proportion.

" Si c'était là le véritable principe de la cristallisation, il ne pouvait manquer de régner aussi dans les cristaux des autres substances ; chacune d'elles devait avoir des molécules constituantes identiques, un noyau toujours semblable à lui-même, et des lames ou des couches accessoires, produisant toutes les variétés. M Haüy ne balance pas à mettre en pièces sa petite collection ; ses cristaux, ceux qu'il obtient de ses amis éclatent sous le marteau : partout il retrouve une structure fondée sur les mêmes lois. Dans le grenat, c'est un tétraèdre ; dans le spath fluor, c'est un octaèdre ; dans la pyrite, c'est un cube ; dans le gypse , dans le spath pesant la barytine ce sont des prismes droits à quatre pans, mais dont les bases ont des angles différents, qui forment les molécules constituantes ; … les faces extérieures se laissent toujours concevoir comme résultant du décroissement des lames superposées, décroissement plus ou moins rapide et qui se fait tantôt par les angles, tantôt par les bords. Les faces … ne sont que de petits escaliers … ; qui paraissent planes à l'œil à cause de leur ténuité. Aucun des cristaux qu'il examine ne lui offre d'exception à sa loi. Il s'écrie une seconde fois, et avec plus d'assurance : Tout est trouvé ! " . [Georges Cuvier, Eloge historique de Haüy, in Recueil des éloges historiques, Paris, 1861, p. 262-264]

Il y aura un troisième cri " tout est trouvé ! " quand, appliquant le calcul au décroissement postulé des couches de molécules, Haüy trouva des mesures d'inclinaison des faces confirmées par l'expérience. Et Cuvier de conclure : " Haüy est … le seul véritable auteur de la science mathématique des cristaux. Suivant l'exemple de tous ceux qui ont véritablement servi les sciences… il a confirmé sa théorie, en montrant qu'elle explique réellement d'une manière rigoureuse les phénomènes connus, et qu'elle prévoit avec précision les phénomènes possibles … il a créé l'ensemble des détails d'une science nouvelle " . [Georges Cuvier, Rapport historique sur les progrès des Sciences depuis 1789, Paris, Verdière, 1828.]

Découverte fortuite. Un homme seul - préparé par des études préalables et à l'esprit aiguisé - prête attention à une observation facilement accessible à chacun, mais dont la particularité avait échappé à tous. Expérience reproduite systématiquement sur tous les minéraux disponibles. Principe unique déduit - la structure - qui explique les formes des cristaux, l'inclinaison possible des faces, qui permet les calculs, confirmés par les mesures. Fondation d'une science nouvelle : la cristallographie. Dans la structure de ce récit s'intègrent deux grands thèmes de l'art du conte : un événement inattendu et un travail opiniâtre conduisent à une juste récompense. Mais l'unité de lieu, de temps et d'action - les trois principes cardinaux de la tragédie classique - sont eux aussi respectés… comme le sont ceux de la méthode hypothético-déductive idéalisée : observations, théorie, prévisions, confirmation expérimentale… N'est ce pas un peu trop ? D'évidence, Cuvier nous propose un " récit d'origine " destiné à prendre place aux côté du lustre de Galilée et de la pomme de Newton dans la galerie des histoires édifiantes censées marquer l'évolution de la science. Mais la lente élaboration et la vie des concepts, la fécondité née de controverses et confrontations, la richesse de la pensée scientifique, ne trouvent pas leur compte dans cette reconstruction. Cette fable masque, remplace, occulte le riche travail d'intellection mené pour comprendre pourquoi les cristaux possèdent des faces naturelles régulières, un travail dans lequel l'œuvre d'Haüy s'inscrit et dont nous allons rétablir brièvement les étapes, espérant contribuer à replacer l'art du conte à la place qui est la sienne.

Au sujet des cristaux, posons quelques jalons dans l'histoire de la science moderne : Johann Kepler (1609) s'émerveille devant les formes régulières des flocons de neige, des cristaux de quartz, de mica… Dans un petit opuscule, la Strena… il les explique à partir de trois types d'arguments : à Aristote, il emprunte l'idée d'une origine liquide des minéraux, à Platon la conception que les formes sont les reflets de l'âme de la Terre - la géométrie étant l'archétype de la beauté, la signature de Dieu - , mais il introduit aussi une troisième raison : celle de la nécessité matérielle, les formes régulières seraient causées par l'entassement compact de petites parties symétriques et invisibles. [Johann Kepler, Strena…, 1609. Traduction française de Robert Halleux, L'étrenne ou la neige sexagulaire, Paris, CNRS/Vrin, 1975.]

René Descartes (1637), dans ses Météores, imagine que les corps sont " …composés de plusieurs petites parties de diverses figures et grosseurs, qui ne sont jamais si bien arrangées, ni si justement jointes ensemble, qu'il ne reste plusieurs intervalles autour d'elles ; et que ces intervalles ne sont pas vides , mais remplis de cette matière fort subtile, par l'entremise de laquelle j'ai dit ci-dessus que se communiquait l'action de la lumière " [René Descartes, Les météores, discours I, Leyde 1637, in Charles Adam et Paul Tannery, Œuvres de Descartes, Paris, Vrin, 1956, tome VI, p. 158-159]. Etendant et modifiant cette vision cartésienne du monde - le monde est plein, des tourbillons l'animent, tout y est expliqué par des raisons de géométrie -, Robert Hooke (1665) estime que les cristaux sont remplis par l'éther, qui permet la propagation des pulsations de la lumière [Robert Hooke, Micrographia ..., Londres 1665, fac similé New-York, Dover, 1961, p. 97]. Cet éther circule entre les petites parties sphériques des corps dont l'assemblage régulier explique les figures géométriques que présentent les germes cristallins et les sels. Hooke observe ceux-ci au microscope et il en décrit la croissance . C'est encore en étant fidèle au cartésianisme que Christiaan Huygens - à la suite d'Erasme Bartholin - étudie la calcite et l'étrange double réfraction de la lumière qu'elle présente. Il met en relation ce dédoublement des images sur lesquelles la calcite est posée avec les angles des faces naturelles du " spath d'Islande ", avec les formes qu'il présente, avec ses clivages, en infère que ces différentes propriétés sont dues à une seule cause : la disposition régulière de petits sphéroïdes - qui ne sont peut-être pas jointifs - entre lesquels circule l'éther. Il généralise en considérant les figures que présentent les flocons de neige, le quartz, le mica, les sels et conclut : " Il semble qu'en général la régularité, qui se trouve dans ces productions, vient de l'arrangement des petites particules invisibles dont elles sont composées " [Christiaan Huygens, Traité de la lumière (1690), Paris, Dunod, 1992]. Mieux, s'appuyant sur cette identité, il met en évidence que le quartz est biréfringent et il parvient, sur la calcite, à préciser par le calcul l'orientation de ses " sphéroïdes plats ". Il peut alors déduire de sa théorie ondulatoire de la lumière certaines propriétés optiques qui découlent de cette orientation (variation de la biréfringence en fonction de l'orientation, absence de celle-ci dans une direction) (Fig. 1). Ces propriétés n'avaient jamais été observées ; il les vérifie de façon précise par l'expérience .

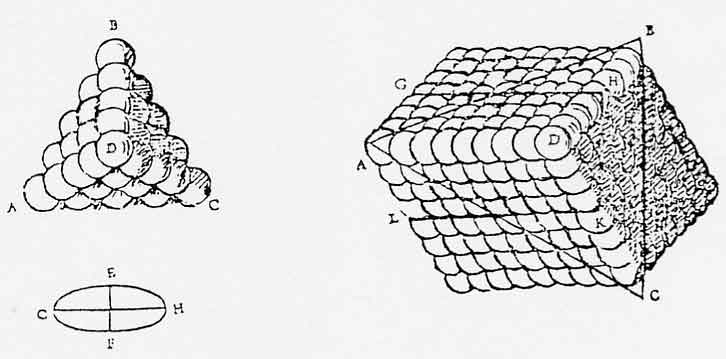
Figure 1. Christiaan Huygens : hypothèse d'une structure de la calcite déduite de l'étude de la symétrie des propriétés physiques. (Traité de la lumière, 1690, chap. 5).

L'autorité de Newton va ruiner ces déductions : ne pouvant admettre que la lumière est une vibration de l'éther mais postulant que l'espace est vide, que la lumière est constituée de petits corpuscules invisibles à l'œil nu qui, d'évidence, traversent les corps transparents en ligne droite, il conclut que les solides sont constitués de petites masses fort éloignées les unes des autres de manière à laisser passer librement les rayons. Ces parties constitutives des corps s'attirent par gravité, se repoussent et se maintiennent à distance sous l'effet d'une autre force. La calcite n'a-t-elle pas une telle structure ? Les corpuscules de lumière ne possèdent-ils pas différents côtés doués de différentes propriétés ? [10) Isaac Newton, Traité d'Optique, traduit par M. Coste, Paris, Montalant, 1722, question XXVI]. Et Newton reproduit les expériences de biréfringence, donne de la double réfraction de la calcite des mesures différentes de celles de Huygens , réduisant les prévisions de celui-ci à l'état de chimères…

Toutes ces conclusions liées à l'établissement au XVIIe siècle des " grands systèmes " de Descartes et Newton, vont intervenir dans l'évolution des conceptions de René-Just Haüy sur les cristaux, non dans leurs naissance : Haüy les ignorait quand il commença ses travaux.

La sphère culturelle dans laquelle vivait Haüy au début de ses études était celle du " Jardin du Roy " (qui venait d'être réorganisé), d'habitudes d'herborisation, de cours publics de sciences naturelles… témoignent d'un grand mouvement qui anime le XVIIIe siècle : contre la prétention des " grands systèmes " à vouloir expliquer tout mécaniquement - même la vie - s'élèvent bien des savants et philosophes. Le courant des " Lumières " va, par exemple, être en partie l'héritier de John Locke et de Nicolas de Malebranche.

Pour Locke (1690), la connaissance a sa source dans les seules données de l'expérience, elle procède de l'analyse des phénomènes, et si la détermination d'un " système du monde " reste l'objectif à atteindre, il est un idéal qui, pour être conquis, ne peut délaisser les patientes analyses. Dès lors, la philosophie de Newton est considérée comme incomplète puisque l'attraction universelle n'est explicable qu'en théologie. Il faut mettre l'accent sur l'empirisme et trouver dans des raisons non mécaniques de nouvelles perspectives pour la science. Selon Locke, l'entendement humain provient de deux sources : d'une part les objets extérieurs, qui lui fournissent les qualités, d'autre part les perceptions et l'esprit, qui fournissent les idées. Il existe deux sortes de qualités : les qualités premières (solidité, étendue, figure, nombre, mouvement…), les qualités secondes (goûts, odeurs, sons, couleurs…) produites en nous par les qualités premières. Pour connaître, il faut partir à la découverte des propriétés sensibles : nous devons rejeter foi, croyance, probabilité. La vérité n'est que la concordance entre ce que nous appréhendons : donner à notre connaissance cette limite, c'est assurer la tolérance.

Le siècle se passionne pour Locke, le pratique, l'admire. En revenant à l'expérience, aux sensations, il contribue à déchaîner l'explosion des recherches sur tout ce qui avait été délaissé par les " grands systèmes " : la chaleur, l'électricité, le magnétisme, la nature, la vie… L'histoire des sciences naturelles devient moment de l'histoire de toutes les sciences, une histoire à laquelle participent savants et philosophes, déistes et athées, curieux et oisifs. Les cabinets de curiosité, les collections se constituent. Dans les salons, on élabore, discute, propose les idées les plus riches et les plus folles. Minéraux et cristaux sont objets de cet engouement.

Influencés par la mode, les cartésiens vont décrire précisément les " qualités " des cristaux, tenter d'expliquer leurs propriétés microscopiques, espérer en déduire la logique du fonctionnement par laquelle toutes les actions mécaniques s'enchaînent. Les newtoniens procèdent aux mêmes études afin de déduire la géométrie des particules ultimes de la matière, d'aborder - peut-être - l'étude de la " force répulsive " qui les maintient à distance les unes des autres. Les chimistes participent aussi activement à cette recherche, tandis que les " descripteurs " et les " sensualistes " veulent se passer de la trop complexe chimie et fondent leurs études sur telle ou telle propriété observable (la couleur de la trace laissée sur la porcelaine, le happement à la langue, l'odeur, la couleur…).

Il manque en France un ouvrage général. Le baron d'Holbach s'en émeut et traduit (1753) le Traité de Minéralogie de Wallerius (1747) qui obtient " dans toute l'Europe un succès mérité et durable ; il donnait un aperçu philosophique d'une science dont chaque savant n'avait eu jusqu'à présent qu'une vue fragmentaire et incomplète … il met le public au courant de toutes les interrogations que l'examen attentif des produits de la croûte terrestre pose à la raison humaine " [Hélène Metzger, La genèse de la science des cristaux, Paris, Blanchard rééd. 1969, p. 58-59]. Dans cet ouvrage, nulle méthode ou idée générale : des coups de sonde, parmi lesquels la recherche du principe constituant responsable de la forme des pierres angulaires ; des descriptions précises et claires des minéraux, auxquelles tout amateur peut se reporter pour identifier les échantillons de sa collection, où une attention particulière est portée à la morphologie des cristaux. Bientôt des dictionnaires apparaissent, renseignent les curieux, deviennent à la mode. Mais pour présenter sa collection, il faut classer. Wallerius utilise une classification des minéraux d'après leur composition chimique. Linné, dans son Système de la Nature (1737) préfère prendre en considération la seule forme cristalline, de manière à guider la trop complexe chimie. Et René-Just Haüy lit Linné afin d'impressionner son ami Lhomond dans leurs herborisations communes.

Bientôt l'intérêt de René-Just Haüy pour la botanique est remplacé par la minéralogie grâce au cours de Daubenton, qui fait des cristaux l'assemblage de " molécules de la matière inorganique qui nage dans un fluide " et qui " s'approchent, se réunissent en vertu de la force attractive lorsqu'elles disposent du temps, du repos et de l'espace nécessaires " [Cité par René-Just Haüy, in Extrait d'un mémoire sur la structure des cristaux de grenat, Obs. sur la Phys., 19, 1782, p. 366-369]. Dès lors, Haüy va mettre autant de soin à examiner les cristaux qu'il l'avait fait à déterminer les plantes. Observant un des plus communs des minéraux - et celui qui se trouve sous le plus grand nombre de formes - la calcite, il remarque " qu'un cristal de cette variété, qui s'était détaché par hasard d'un groupe, se trouvait cassé obliquement, de manière que la fracture présentait une coupe nette, et qui avait ce brillant auquel on reconnaît le poli de la Nature [C'est un clivage - phénomène très fréquent dans la calcite - que décrit ainsi Haüy]. J'essayai si je ne pouvais point faire, dans ce même prisme, des coupes dirigées selon d'autres sens ; et après différentes tentatives, je parvins à obtenir de chaque côté du prisme trois sections obliques et par de nouvelles coupes parallèles aux premières, je détachai un rhomboïde parfaitement semblable au spath d'Islande, et qui occupait le milieu du prisme " [René-Just Haüy, Essai d'une théorie sur la structure des cristaux, appliquée à plusieurs genres de substances cristallisées, Paris, Goguée, 1784]. Ces essais décrits sont bien loin de la fable - et prouvent qu'Haüy n'a encore rien lu sur la calcite. Haüy continue ses expériences sur d'autres cristaux " assez tendres pour être divisés nettement " : il obtient toujours des " noyaux qui avaient d'autres formes ". On peut supposer que Haüy est enthousiasmé par ses découvertes. Il entreprend des lectures, notamment, nous allons le montrer, celle de Bergman.

" Dans le temps où je commençais à me livrer à l'étude de la structure des cristaux, j'ai eu l'occasion de lire un mémoire de M. Bergman sur la cristallisation " . Voici ce que nous dit Haüy, et de fait, Torbern Bergman (1735-1784) va avoir une influence certaine sur la formation des idées de René-Just Haüy. Ce chimiste suédois publie en 1773 un mémoire sur les formes cristallines et l'origine des spaths [Torbern Bergman, Variae crystallorum formae a spatho ortae, Nova Acta Reg. Soc. Upsal., Upsaline, 1773, vol. I, p. 150 et suiv.]. Ignorant d'évidence les études qu'en avait faites Christiaan Huygens, il a son attention attirée par un de ses élèves, Gahn, sur le fait qu'en brisant un cristal de spath pyramidal, on obtient toujours un noyau rhomboïdal analogue au spath d'Islande (c'est toujours la même observation courante que font les auteurs !). Reprenant cette expérience, montrant qu'il en est de même pour d'autres formes naturelles connues de la calcite, étendant son étude aux grenats, à la pyrite, à la hyacinthe, aux " cristaux basaltiques " (la toumaline et la staurotide), Bergman conclut que tous ces cristaux présentent des formes géométriques naturelles qui dépendent des conditions dans lesquelles les minéraux prennent naissance et croissent : l'observation nous renseigne sur l'histoire de cette formation. Toutes les formes de la calcite peuvent selon Bergman se résumer par l'adjonction à un noyau initial de parallélogrammes successifs dont les angles sont 101½° et 78½°. De même tous les cristaux sont formés de ces mêmes lamelles infiniment minces. Cela permet d'expliquer l'existence des faces planes limitrophes et des clivages.

Bergman " ignore la mesure des angles et s'appuie seulement sur des ressemblances superficielles des habitus, il confond les angles de la calcite rhomboédrique avec ceux du grenat (cubique) et la hyacinthe (tétragonale) " [R. Hooykaas, The historical and philosophical background of Haüy's theory of Crystal Structure, Academiae Analecta, AWLsK, Jaargang 56, 1994, Nr. 2, p. 10]. C'est à la critique de ce travail - dont il a donc bien pris connaissance en même temps qu'il mène ses propres travaux - que va être consacrée la première publication de René-Just Haüy, un Mémoire sur la structure des cristaux de grenat, présenté à l'Académie royale des sciences le 21 février 178113.

Haüy pose d'emblée le sujet de son travail : l'observation des formes cristallines. Celle-ci a donné " aux yeux des Naturalistes un nouvel ordre de connaissances, et leur a fourni de nouveaux sujets d'admirer la puissance suprême, qui dirige la Nature toujours variée et toujours inépuisable dans les jeux de sa fécondité. Ce qu'il y a ici de plus surprenant, c'est de voir souvent parmi les cristaux qui appartiennent à une même substance, une multitude de formes diverses, entre lesquelles on n'aperçoit au premier coup d'œil aucun rapport, et qu'il paraît presqu'impossible de ramener à une même forme. On voit aussi, dans des genres très-distingués entr'eux, des cristaux qui ont une forme commune "13.

Haüy dit vouloir essayer d'écarter toute supposition ou système préalable et ne s'appuyer que sur l'observation et l'expérience. Nous ne nous étonnerons pas de le voir nous rapporter qu'il clive les cristaux avec un instrument tranchant de manière à " détacher des lames qui aient le poli de la nature " ou, à défaut, " rechercher la structure, d'après des raisons d'analogie, et en profitant surtout des stries et des linéaments que l'on observe souvent sur leurs différentes faces, et qui indiquent la position des lames dont ces cristaux sont l'assemblage ". Ce dernier type de déductions, quoiqu'en dise Haüy, est fait au nom des principes postulés (ici l'assemblage de lames), condition toujours nécessaire à l'intelligibilité de l'observation de la nature. Haüy en infère - suivant en cela Bergman - que tous les cristaux de même sorte, quelle que soit leur forme extérieure, sont formés d'un noyau (un cristal que l'on doit regarder comme primitif) et de lames successives, le noyau étant lui même formé de lames. Mais Haüy démontre aussi que Bergman peut avoir tort, notamment lorsqu'il affirme que calcite et grenat ont même noyau. Plus précis, ayant plus souvent recours à la mesure, Haüy démontre que les grenats ont un noyau octaédrique, la calcite un noyau rhomboédrique, le sel marin un noyau cubique… et que les lames détachées ont des figures et proportions selon les diverses variétés du noyau : si celui-ci est rhomboïdal, les lames seront des " rhombes … des demi-rhombes ou des triangles isocèles, qui sont les moitiés des rhombes ".

Ainsi, des formes communes à plusieurs cristaux de genres différents " cachent souvent des structures très différentes entre elles " (le sel marin se divise en cubes, la fluorine en octaèdres), de même que, au contraire, des cristaux de même espèce (la calcite), donc de même noyau, peuvent présenter des formes extérieures différentes par adjonction de lames diverses. Pour démontrer cela, Haüy se lance encore dans des mesures précises d'angles des faces planes : il conçoit quelles lames sont compatibles avec ces faces, calcule par la méthode des sinus les angles plans possibles à partir de l'empilement de lamelles, confirme la possibilité de ces empilements par l'observation. Haüy part donc de l'idée de Bergman, reste dans le cadre d'une géométrie plane, mais démontre que Bergman ne peut pas être aussi général qu'il l'a été et développe - encore de manière bidimensionnelle - ce que va être sa grande idée : les cristaux peuvent se distinguer par la géométrie de leur noyau ; leurs faces extérieures résultent de l'empilement " comme par étages " de lames décroissantes.

Dans un second mémoire, lu la même année à l'Académie, mûri donc en même temps [René-Just Haüy, Extrait d'un mémoire sur la structure des Spaths calcaires. Obs. sur la Phys., 20, 1782, p. 33-39], Haüy détaille ses idées sur la calcite : certains cristaux, de diverses formes extérieures, ont un noyau rhomboïdal " entièrement semblable au spath d'Islande " auquel s'ajoute " un excès de matière " qui est " un assemblage de lames en forme de rhombes … mais incomplètes, soit dans leurs bords, soit dans leurs angles, de manière cependant que ces mêmes lames … peuvent toujours se sous-diviser en un certain nombre … de rhombes entiers … ou de demi rhombes ou de triangles isocèles ".

Toujours de la géométrie plane, avec des mesures précises qui permettent d'expliquer l'existence de cinq des formes les plus communes de la calcite. Ici encore, Haüy note que Bergman ne peut, comme il le fait, assimiler la division du spath calcaire et celle du grenat, mais constate la validité de quelques-unes de ses déductions sur la calcite " en dent de cochon ", - ce qui prouve qu'il ne s'intéresse pas alors aux angles dièdres -, et en rectifie d'autres grâce à ses mesures. Il termine son article en notant : " Je ne prétends pas que tous les cristaux de spath calcaire, quelle que soit leur grosseur, aient commencé chacun par un noyau semblable au spath d'Islande … . Les plus petits cristaux que l'on puisse apercevoir, à l'aide du microscope,… ont la même forme que les plus gros … . Mais il me semble que la structure se combine avec l'accroissement [pour former les cristaux microscopiques] ". L'idée générale n'est pas encore atteinte.

Un des grands minéralogistes français de l'époque est sans aucun doute Jean-Baptiste Romé de l'Isle. Celui-ci observe avec minutie les collections assemblées dans les cabinets et salons, publie des catalogues d'identification raisonnée des minéraux, accorde une importance particulière aux formes extérieures, fait passer de quarante à quatre cents le nombre des formes décrites. Il mesure les angles des faces planes, compare à l'aide de mires les angles dièdres des faces et rédige en 1772 un Essai de cristallographie qui obtient un grand succès [Jean-Baptiste Romé de l'Isle, Cristallographie ou description des figures géométriques, propres à différents corps du Règne Minéral, connus vulgairement sous le nom de Cristaux, Paris, 1772]. Voulant parvenir à mesurer avec précision les angles dièdres que font entre elles les faces des cristaux, il va trouver le mécanicien Carrangeot, qui met au point un " goniomètre d'application " (Fig. 2) : à la base d'un rapporteur sont fixées deux lames. L'une est fixe, l'autre mobile. Les lames s'appliquent sur les faces et permettent de mesurer leurs angles à un tiers de degré près. Muni de cet appareil, Romé de l'Isle revisite sa collection, mesure systématiquement les angles de tous les cristaux qu'il possède, constate que les minéraux présentent toujours des faces qui font entre elles des angles constants dans une même espèce. Il peut alors rédiger et publier, dans l'introduction de sa Cristallographie (1783) ce qui est connu comme la première loi de la cristallographie : la constance des angles dièdres. " Les faces d'un cristal peuvent varier dans leur figure et dans leurs dimensions relatives ; mais l'inclinaison respective de ces mêmes faces est constante et invariable dans chaque espèce " [Jean-Baptiste Romé de l'Isle, Cristallographie ou description des formes propres à tous les corps du Règne Minéral. Paris 1783, tome premier, introduction, p. 93]. Romé de l'Isle peut alors idéaliser les formes cristallines : puisque le développement respectif des faces d'un minéral n'est pas important, autant représenter les cristaux par les modèles où toutes les faces homologues ont même développement . Ainsi, les espèces cristallines peuvent-elles être caractérisées au moyen de trois paramètres : leur densité, leur dureté et leur forme polyèdre. Voilà, note Romé de l'Isle qui s'accorde avec ce qu'annonce Salomon dans le livre de la Sagesse : " Tu prépares tout avec mesure, nombre et poids ", et voilà qui peut fournir un guide pour diriger la trop complexe chimie.

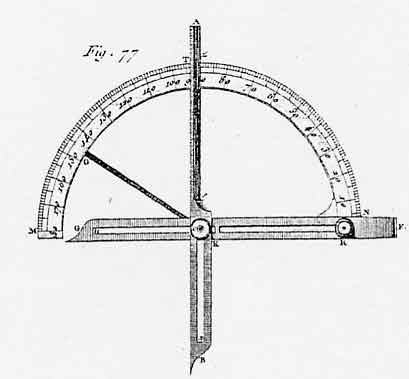
Figure 2. Goniomètre de Carrangeot

Ayant ainsi pu quantifier certaines propriétés sensibles, Romé aspire à fonder une " Nouvelle Science ", la cristallographie. Pour cela, il lit ses devanciers, les critique, poursuit ses propres expérimentations, en induit une réflexion cohérente : les cristaux sont formés de petits corpuscules qui s'approchent les uns des autres lors de la cristallisation, mais restent à distance les uns des autres. Ces corpuscules sont inaccessibles et le resteront peut-être à jamais ; par contre nous pourrons peut être atteindre la plus petite partie que le cristal peut présenter : elle est formée de corpuscules de nature différente, mais possédant toutes les propriétés du cristal - la " molécule intégrante ". Les molécules intégrantes s'empileraient pour donner les cristaux, dont la géométrie nous montre qu'elles peuvent être réparties en six catégories : les six polyèdres convexes qui permettent d'emplir l'espace (le tétraèdre, le cube, l'octaèdre, le parallélépipède rhomboïdal, l'octaèdre rhomboïdal, le dodécaèdre à plans triangulaires). Une opération purement géométrique donne une preuve mathématique de la validité de la déduction : on peut retrouver les formes idéalisées à partir des polyèdres en intersectant les sommets ou les arêtes de ceux-ci par des plans ! Ce sont les " troncatures " et Romé de l'Isle conclut son introduction - avant de passer à la description des minéraux classés selon leur composition chimique (les sels, les acides…) - en précisant bien ce qu'il entend par cristallisation. " Quant au mécanisme interne et caché de la cristallisation, nous sommes encore bien éloignés de pouvoir en rendre compte : c'est un mystère de la Nature, qui, de même que la génération dans les animaux et la végétation dans les plantes, échappe à la curiosité de nos regards. … le meilleur microscope ne vous fera point voir la manière dont s'est opérée cette augmentation. La raison en est simple, c'est que les molécules élémentaires et même les molécules premières intégrantes, qui sont les matériaux que la Nature emploie à la construction de tous les corps, sont, comme je l'ai dit, inaccessibles à nos sens ; et que la plus petite parcelle de matière que nos yeux puissent apercevoir à l'aide du microscope, loin de pouvoir être regardée comme un être simple, est déjà très composée. Tenons-nous en donc à ce que l'observation nous présente, si nous ne voulons pas substituer les rêves de notre imagination au silence majestueux de la Nature sur les grands principes " .

Cette dernière phrase vise René-Just Haüy : dans la préface qui précède l'introduction de l'ouvrage, Romé de l'Isle est moins allusif. " Je dis qu'un tel cristal est tronqué dans ses angles solides ou dans ses bords, quoique je sache très bien que la Nature ne commence point par faire un cristal entier, pour le tronquer ensuite plus ou moins… Des novateurs en cristallographie, qu'on peut avec raison nommer Cristalloclastes (brise-cristaux), s'imaginent avoir fait une grande découverte en nous annonçant.. que la Nature ne tronque point " et, plus loin : " Je n'ignore pas, qu'à l'imitation du célèbre Bergman, quelques physiciens s'occupent actuellement parmi nous à démontrer par des figures et des calculs géométriques, le mécanisme de la construction particulière à quelques cristaux qui se laissent diviser facilement à l'aide d'un instrument tranchant : leurs tentatives méritent certainement d'être encouragées ; mais je crois qu'avant de chercher à pénétrer le travail secret de la Nature … il faudrait commencer par étudier toutes les variétés de formes dont une espèce est susceptible … C'est ainsi que M. l'Abbé Haüy, Professeur au Collège du Cardinal le Moine, ayant observé que le grenat a vingt quatre facettes " (et Romé démontre qu'Haüy n'est pas général dans son étude sur le grenat)…Il peut donc conclure : " Cet exemple doit suffire pour nous mettre en garde contre ces prétendues démonstrations géométriques dont on fait tant de bruit " .

Les certitudes d'un praticien expérimentaliste (Romé de l'Isle), s'en tenant aux mesures d'angles dièdres et aux cas concrets observés, contre les extrapolations générales d'un géomètre qui s'en tient encore aux empilements de plans (R.-J. Haüy) : voici les termes du débat posé… des termes qui vont se modifier avec la publication en 1784 par Haüy de son Essai d'une théorie sur la structure des cristaux.

Dès les premières lignes de son Essai…, René-Just Haüy réaffirme sa position " La théorie que je propose dans cet Ouvrage, est fondée sur l'accord de l'observation avec le calcul, dont je ne pouvais me dispenser de faire usage, pour traiter, avec quelques succès, une matière où tout est, pour ainsi dire, proportion et régularité " . Attendons-nous donc à voir se développer un raisonnement géométrique vérifié par l'expérience. Et Haüy de préciser d'emblée le but qu'il poursuit : " on peut se proposer deux choses dans l'étude des cristaux : l'une, de tirer de leurs différentes formes, des caractères distinctifs, pour reconnaître les minéraux ; l'autre, de comparer ces formes les unes avec les autres, d'en saisir les rapports et les différences, et même d'expliquer, s'il se peut, le mécanisme interne de leur structure ; de réduire, en un mot, la Cristallographie à une Science qui ait des principes fixes, d'où l'on puisse tirer des conséquences propres à répandre du jour sur une matière jusqu'ici enveloppée de tant d'obscurités ".

" A l'égard du premier de ces objets, il est certain d'abord que jamais on ne pourra faire de la Cristallographie la base d'une distribution méthodique des minéraux … . Les formes ne peuvent … être employées que subsidiairement, et comme caractères secondaires, avec ceux qui se tirent de la cassure, de la dureté, du poli, etc… ".

" Quant au second point, qui consiste à établir une théorie sur la Cristallisation, il m'a paru que l'on avait trop négligé de faire les recherches qui pouvaient conduire à ce but … . Cependant, en y regardant de plus près, on observe que beaucoup de formes, qui d'abord avaient paru semblables dans les cristaux de nature diverse, diffèrent entr'elles par les angles planes de leurs faces … . On remarque de plus que ces angles et ces axes sont constants dans la même variété du cristal … . On aperçoit des passages d'une forme à l'autre, des gradations marquées, qui indiquent des rapprochements que l'on n'avait pas soupçonnés d'abord. Ce sont ces observations, suivies avec soin, et souvent répétées, qui m'ont fait naître le désir et l'espérance de faire un nouveau pas dans la connaissance des cristaux, et de répandre quelque jour sur cette matière … ". " Au reste, mon dessein n'a pas été de rechercher la manière dont agissent les forces primitives auxquelles est soumise la cristallisation … . Je me suis borné à un genre de recherches plus à ma portée, en me proposant de déterminer la forme des molécules constituantes des cristaux, et la manière dont elles sont arrangées entr'elles dans chaque cristal. C'est cette combinaison que j'appelle structure ; et l'on verra, dans le cours de cet Ouvrage, qu'elle est soumise à un petit nombre de lois, dont les modifications combinées produisent toutes les variétés de formes que l'on observe dans les cristaux ".

" Les résultats auxquels conduit une pareille théorie, ne pouvaient être constatés qu'à l'aide de la Géométrie " .

Haüy répond point par point à Romé de l'Isle : il ne veut pas s'occuper de déterminer ce qu'est la cristallisation ; il ne va se soucier que de la structure des cristaux ; celle ci est formée par " l'aggrégation " de " molécules constituantes " initialement " suspendues… dans le fluide où elles étaient en dissolution ". Inutile d'instruire donc un procès contre ceux qui chercheraient à " pénétrer le travail secret de la nature " : l'étude découvre " aux yeux des Naturalistes un nouvel ordre de faits intéressants, où l'on voit jusqu'aux moindres molécules de la matière soumises, par une Sagesse suprême, à des lois toujours subsistantes, d'où naissent l'harmonie et la régularité ". C'est l'existence des lois - le comment - qui est sujet de l'étude, non le pourquoi.

Parmi les lois, Haüy indique au passage, nous l'avons vu, la constance des angles, découverte par Romé de l'Isle, qui n'est jamais cité dans l'Essai… Suivant Romé, il va remplacer les lames et lamelles des années 1780-1782 par des volumes décrits et généralisés grâce à la géométrie. Certain de l'existence d'une " sagesse suprême " qui donne une harmonie pouvant être décrite par la géométrie, Haüy va étendre les lois qu'il trouve sur des cristaux particuliers à l'ensemble des cristallisations. Voici un acte fondateur par lequel Haüy dégage la cristallographie des sciences naturelles et la rattache aux mathématiques mixtes de son temps….

Ainsi, l'Essai s'appuie sur une méthode : les cristaux qui peuvent être divisés le sont et permettent de dégager les molécules constituantes, d'en définir la géométrie. Si les cristaux ne se prêtent pas à la division, ce sont les stries présentes sur les faces qui vont conduire à la déduction de ces formes. Si aucune de ces propriétés n'apparaît, des " raisons d'analogie " permettent à Haüy d'inférer la " forme primitive " (de même géométrie que la " molécule constituante "). La considération géométrique de l'assemblage tridimensionnel de ces formes conduit à l'explication de toutes les faces des cristaux : lorsque les couches successives contiennent autant de molécules dans les trois directions de l'espace, la géométrie de la forme obtenue est la même que la primitive. Si des décroissements se manifestent, il se produit des " degrés d'escalier " invisibles au microscope qui constituent des faces. Ces degrés peuvent avoir un " pas " formé d'une, deux, trois molécules constituantes. Pour déterminer la solution particulière que présente un cristal, il faut calculer les différentes possibilités de décroissements. " C'est alors que la géométrie devient indispensable ". En mesurant ensuite les angles des faces du cristal, la loi de décroissement, ainsi que la forme postulée de la molécule constituante sont confirmés. Les cristaux qui présentent de telles faces différentes de celles de la " forme primitive " constituent ce que Haüy appelle des " formes secondaires ". " Pour vérifier sur le cristal même les angles trouvés à l'aide du calcul, je me suis servi d'un instrument que j'ai fait construire exprès avec tout le soin possible " nous dit Haüy, qui ne cite ici encore ni Romé de l'Isle, ni Carangeot. Les différences trouvées avec les résultats de la trigonométrie " étaient trop légères pour être attribuées à d'autres lois de décroissement ". Nous reviendrons sur cette affirmation.

Finalement, tout le travail d'Haüy " consiste à résoudre, dans chaque cas particulier, ce problème général : Etant donné un cristal, déterminer la forme précise de ses molécules constituantes, leur arrangement respectif, et les lois que suivent les variations des lames dont il est composé ".

Le seul guide à prendre est la structure, mais " l'étude des cristaux ne peut … servir … qu'à lever une partie de la difficulté " : des minéraux différents peuvent avoir des molécules constituantes semblables entr'elles mais des molécules élémentaires différentes… et on ne peut atteindre celles-ci " malgré les progrès sensibles qu'a fait la Chimie dans ces derniers temps " .

Ainsi, dans un champ d'étude très vaste, trop difficile à traiter, Haüy vient d'opérer une réduction des propriétés du réel : parmi toutes les propriétés observées des cristaux (couleur, goût, dureté, densité, affinités chimiques, formes…), il sélectionne une propriété : la constance des angles. Celle-ci lui permet d'introduire un modèle, " la molécule constituante ", qui ne possède pas obligatoirement de réalité en soi mais permet de mettre en œuvre une géométrisation rendant compte des données numériques relatives à la propriété choisie. La " molécule constituante " n'est donc pas seulement figurative - et à la limite triviale - : elle joue le rôle d'un opérateur sélectif en ce qu'elle sépare le " non-pertinent " du " pertinent " [Robert Locqueneux, Bernard Maitte, Bernard Pourprix, Formalisation et Expérimentation en physique, Fundamenta Scientiae, vol. 7, 1987, n° 3/4, p. 423-438].

Le succès de l'Essai est grand parmi les tenants des " mathématiques mixtes ", mais les calculs développés par Haüy - qui a dû aborder de manière autodidacte une discipline (les mathématiques) qui lui était jusqu'alors inconnue - dissuadent les naturalistes. A partir de la publication de l'Essai…, ainsi appelé parce qu'il ne fait qu'esquisser une théorie dont la nouveauté fait qu'elle est " très susceptible d'être perfectionnée ", vont avoir lieu les réunions regroupant Lagrange, Laplace, Fourcroy, Guyton de Morveau, Berthollet dans la chambrette du Cardinal Lemoine. Geoffroy Saint-Hilaire sert de préparateur et de secrétaire à ces réunions. Dès lors, Haüy enrichit sa collection de minéraux, de modèles en bois, grâce auxquels il peut raisonner sur chaque cas particulier… et conseille à tous ses lecteurs de construire ou d'acquérir des modèles, qui vont se diffuser dans toute l'Europe.

De 1784 à sa mort survenue en 1822, Haüy va publier plus de cent articles et ouvrages sur les cristaux. Nous ne pouvons qu'évoquer rapidement l'évolution de ses idées. Une première étape est marquée par la publication en 1792 de l'Exposition abrégée de la théorie sur la structure des cristaux où, note Haüy, " Les recherches successives que j'ai faites pour étendre et perfectionner cette théorie, l'ont élevée à un degré de généralité, dont je ne l'avais pas crue d'abord susceptible, mais qui ne peut être bien saisi qu'à l'aide du calcul analytique " . Que trouve-t-on de nouveau et de plus général dans cet ouvrage ?

Après la description des divisions mécaniques et des observations qui permettent, pour une variété minérale de distinguer la " forme primitive " et les " formes secondaires ", multiples, Haüy dit vouloir réduire cette diversité par l'unité de la théorie. Or la division du cristal ne peut être - même par la pensée - menée à l'infini : on arrive obligatoirement " à un terme, passé lequel on arriverait à des particules si petites, qu'on ne pourrait plus les diviser, sans les analyser, c'est-à-dire, sans détruire la nature de la substance " . Ce terme ce sont les " molécules intégrantes " - Haüy reprend l'appellation utilisée par Romé de l'Isle - mort en 1790 - mais sans citer celui-ci ; leur division donnerait les éléments chimiques dont elles sont constituées.

Les diverses formes secondaires résultent de l'arrangement tridimensionnel de mêmes molécules intégrantes au sein d'une même structure. Haüy en donne une idée en montrant que le dodécaèdre rhomboïdal peut être considéré comme l'empilement de cubes dont les faces sont déterminées par une même loi de décroissement (Fig. 3). Ses raisonnements s'appliquent maintenant à une géométrie dans l'espace, mais prise " lame par lame ". Celles-ci constituent toujours des escaliers invisibles puisque " l'on peut même supposer les cubes composants si petits, que ces cannelures deviennent nulles pour nos sens, et que les faces des pyramides paraissent parfaitement unies " .

Pour chacun des minéraux, il faut abstraire une " loi de décroissement " et une molécule intégrante, ce qui nécessite observations, mesures, calculs, prévisions, vérifications. Par des calculs faits en trigonométrie plane et des mesures effectuées au moyen du goniomètre d'application, Haüy parvient à illustrer que son élégante conception rend compte de diverses formes secondaires, idéalisées à la manière de Romé de l'Isle - toujours non cité pour cet apport - , notamment pour le dodécaèdre pentagonal de la pyrite. Par contre Haüy tient à noter que " M. Verner et M. Romé de l'Isle ont confondu [ce dodécaèdre] avec le dodécaèdre régulier de la géométrie "34. Il insiste : " Si ces deux minéralogistes célèbres eussent mis plus de géométrie dans leur manière de considérer les cristaux, ils auraient aperçu une distinction très marquée entre ces deux dodécaèdres … . On peut juger ainsi combien l'usage du calcul est important " .

Empiler des lames successives est une opération malcommode. Une fois la preuve faite que l'on peut rendre ainsi compte de la multiplicité des formes secondaires, autant procéder à l'envers comme l'avait fait Romé de l'Isle : les inclinaisons des faces étant connues ainsi que la molécule intégrante, Haüy montre que les faces peuvent être géométriquement considérées comme des plans intersectant des angles ou des arêtes de la molécule intégrante (elles sont produites par des " décroissements sur les angles ", des " décroissements sur les arêtes " ou des " décroissements mixtes " ) ; un pas de plus vers l'unité souhaitée.

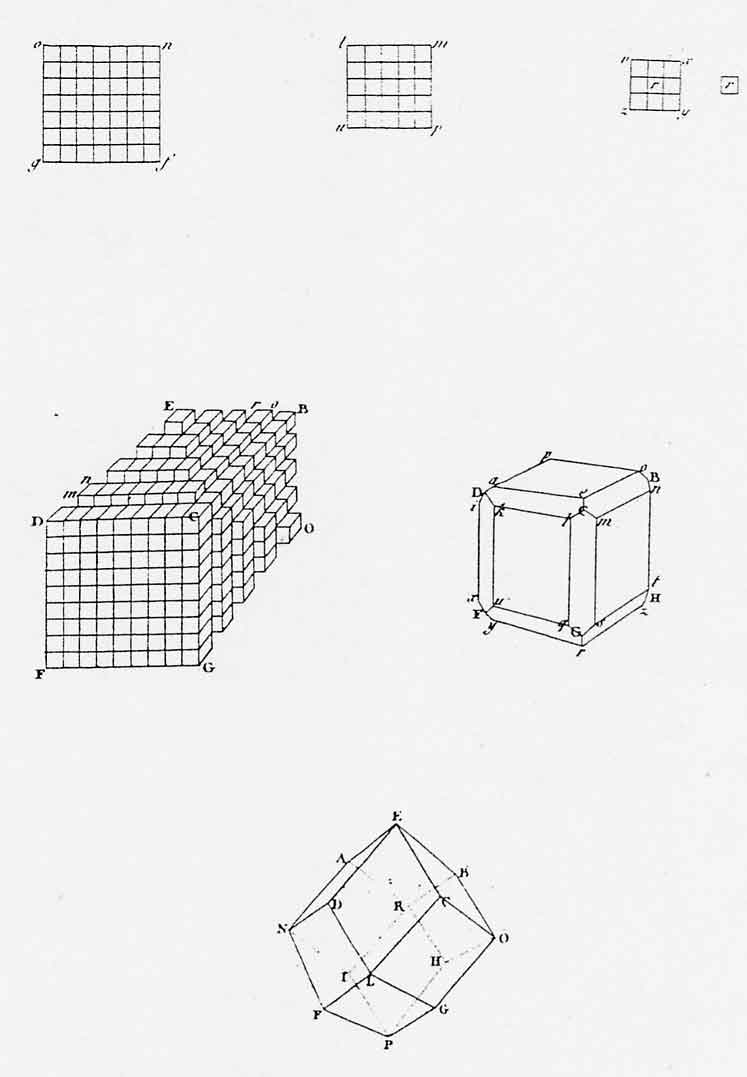
Figure 3. Les couches de décroissement conduisent à la cristallisation d'un rhombododécaèdre. On peut retrouver plus simplement celui-ci par la géométrie : en tronquant les arêtes de la forme primitive cubique. (Haüy : Exposition abrégée…).

Il reste à définir pour tous les cristaux connus, toutes les formes primitives possibles. Ce n'est pas un problème facile. Haüy voudrait obtenir une grande simplicité. Il parvient à réduire à six le nombre des catégories : " le parallélépipède en général, lequel comprend le cube, le rhomboïde et tous les solides terminés par six faces parallèles deux à deux ; le tétraèdre régulier ; l'octaèdre à faces triangulaires, le prisme hexagonal, le dodécaèdre à plans rhombes, et le dodécaèdre à plans triangulaires isocèles " . Romé de l'Isle distinguait déjà dans sa cristallographie six types de " molécules intégrantes " empilées. Haüy en regroupe certaines (le parallélépipède en général), et distingue en plus le dodécaèdre rhomboïdal et le prisme hexagonal.

Le " point le plus délicat de la théorie " est ailleurs : en se bornant à effectuer (par la pensée) sur tout cristal six sections parallèles deux à deux, on obtient toujours un noyau parallélépipédique qui est souvent la molécule intégrante. " Mais il est certains minéraux, où le parallélépipède est divisible, ainsi que le reste du cristal par des coupes ultérieures réelles faites dans des sens différents de ses faces "38. Ainsi, des cubes de fluorine peuvent être divisés de manière diagonale : on extrait alors un octaèdre et douze tétraèdres " sans jamais pouvoir réduire à l'unité le résultat de la division. Or les molécules d'un cristal étant nécessairement similaires, il m'a paru probable que la structure était comme criblée d'une multitude de vacuoles occupées soit par l'eau de cristallisation, soit … , en sorte que s'il nous était donné de pousser la division jusqu'à sa limite … l'une des deux espèces de solides dont il s'agit disparaîtrait, et tout cristal se trouverait uniquement composé de molécules de l'autre forme " . L'idéal géométrique est encore marqué par la pesanteur des faits matériels.

Et Haüy de continuer à rechercher la beauté : " En adoptant donc le tétraèdre, dans les cas douteux … on réduirait en général toutes les formes de molécules intégrantes à trois formes remarquables par leur simplicité, savoir le parallélépipède qui est le plus simple des solides dont les faces sont parallèles deux à deux, le prisme triangulaire qui est le plus simple des prismes, et le tétraèdre qui est la plus simple des pyramides … . Au reste, je m'abstiendrai de prononcer sur ce sujet " . Haüy peut alors revenir sur la cristallisation : la molécule intégrante d'un rhombododécaèdre est un cube. Cela ne veut pas dire que le cube se forme d'abord et s'accroît progressivement pour donner, par des lames de superposition, le dodécaèdre. " Il paraît prouvé, au contraire, que dès le premier instant, le cristal est déjà un très petit dodécaèdre, qui renferme un noyau cubique proportionné à sa petitesse, et que dans les instants suivants le cristal s'accroît, sans changer de forme " . " Mais il resterait de nouvelles recherches à faire, pour remonter encore de quelques pas vers les lois primitives auxquelles le Créateur a soumis la cristallisation, et qui ne sont elles-mêmes autre chose que les effets immédiats de sa volonté suprême " .

C'est à ce point de ses réflexions qu'en est Haüy lorsqu'il professe ses cours à l'Ecole normale de l'an III, mais il a aussi enrichi sa théorie grâce à de très nombreuses études effectuées sur des minéraux particuliers. Il est ainsi amené à s'intéresser à la double réfraction de la calcite (1788 et 1792), du quartz (1792), d'autres minéraux (1793) : il lit alors à ce sujet Christiaan Huygens et Isaac Newton, aborde la théorie de la lumière. Il étudie aussi les propriétés électriques des minéraux (1785), discute de la validité de la loi de Coulomb, publie un ouvrage l'Exposition raisonnée de la théorie de l'électricité et du magnétisme d'après les principes d'Aepinus (1787). Celui-ci ayant découvert que, chauffée, la tourmaline laisse apparaître des charges électriques aux extrémités des pyramides qui terminent ses cristaux (1792), Haüy étend cette découverte de la " pyroélectricité " aux relations qu'entretiennent structure cristalline et propriétés physiques d'un cristal. Il s'intéresse aussi au calorique. Les cristaux l'amènent donc à revisiter l'ensemble de la minéralogie et forgent sa compétence en physique. Ce sera la justification de sa désignation comme enseignant à l'Ecole normale de l'an III.

Dans ce cours, Haüy commence par décrire la cristallisation telle que l'on pourrait la suivre si nous y avions accès : " Les molécules salines, tenues en dissolution dans un fluide, se rapprochent à la faveur de l'évaporation … par leurs attractions mutuelles, elles s'unissent de préférence par certaines faces ; elles forment des groupes d'abord imperceptibles, mais qui s'accroissent bientôt jusqu'au point de devenir sensibles à l'œil. Alors on voit paraître à la surface du liquide […] une multitude de petits corps réguliers " [René-Just Haüy, Leçons de physique, in Leçons de l'Ecole normale de l'An III]. L'art du pédagogue est de conter et d'entraîner ses étudiants à suivre la marche de la nature, telle que la théorie conduit Haüy à dire comment elle procède. Mais, continue Haüy, les minéraux - c'est une différence avec les fleurs, par exemple, qui sont semblables partout où elles poussent - sont souvent " d'une même substance, affectent diverses formes … qui paraissent être entièrement étrangères les unes à l'égard des autres " . Et Haüy présente aux étudiants de telles formes et leurs modèles en bois idéalisés par la géométrie. Mais, note-t-il, une autre difficulté vient de ce que " des substances très différentes … présentent absolument la même forme " . Et Haüy de tracer rapidement l'histoire des interprétations de l'existence des faces cristallines, de Linné à " l'idée-mère " de Bergman et aux études de Romé de L'Isle à qui, devant l'immense auditoire assemblé, Haüy rend un hommage appuyé pour la détermination de la forme primitive, pour la notion géométrique de troncatures, pour sa loi de constance des angles. Haüy de conclure : " En un mot, sa cristallographie est le fruit d'un travail immense par son étendue, presque entièrement neuf par son objet, et très précieuse par son utilité " - première reconnaissance du mérite de Romé de l'Isle, qui sera reprise textuellement dans le traité de minéralogie de 1801 [René-Just Haüy, Traité de Minéralogie, Paris, 1801, Tome 1, p. 17].

Haüy peut maintenant tracer sa propre théorie, " fondée sur le même principe que celle de Bergman et qui fait concourir à la fois l'observation et le calcul à la détermination des lois auxquelles est soumise la structure des cristaux " . Il y entraîne à nouveau ses auditeurs à " la manière dont un observateur pourrait y être conduit ", par les clivages de la calcite, de la fluorine, par l'observation de stries, par extrapolation " dans le cas où l'observation se tait ", en postulant alors une marche constante de la nature. Ainsi, le professeur peut affirmer que " tous les cristaux originaires d'une même substance, quelque variées … [que] soient leurs figures, ont un noyau constant … . Ce noyau est [la] forme primitive … les formes secondaires sont celles qui diffèrent de la forme primitive " . Toutes les formes - simples ou secondaires - peuvent être subdivisées par la pensée jusqu'à une partie " d'une extrême petitesse, et que l'on ne pourrait plus diviser ultérieurement sans les analyser, c'est-à-dire sans détruire la nature de la substance ". Cette plus petite partie physique est la " molécule intégrante ". " Dans la réalité un cristal n'est autre chose qu'un assortiment de molécules intégrantes juxtaposées - depuis le centre jusqu'à la surface " : nous reconnaissons là les déductions de l'Exposition abrégée… Haüy peut alors introduire les décroissements qui expliquent les faces, et convaincre de leur pertinence ses élèves grâce à des exemples montrés sur des modèles " que nous réduirons ensuite par la pensée en solides imperceptibles, pour ramener, si j'ose ainsi parler, notre maçonnerie grossière à l'architecture infiniment délicate de la nature " . Après avoir appris à voir avec les yeux de la théorie, les auditeurs peuvent aisément admettre qu'il est plus facile encore de partir de la forme simple - par exemple cubique - pour parvenir aux formes secondaires - par exemple le dodécaèdre rhomboïdal - par décroissement sur les bords. Cette opération intellectuelle simplifie le raisonnement. Les décroissements postulés permettent de prévoir les angles de faces. La mesure de ceux-ci prouve la validité de la loi, aux imprécisions de mesures près.

Le professeur peut alors revenir à la cristallisation, dire sa quasi-certitude que " dès le premier instant, l'embryon du cristal naissant était déjà semblable à ce cristal parvenu à son entier accroissement " , mais il ajoute - et c'est nouveau - : " Nous pensons cependant, qu'il est possible qu'un cristal, qui serait déjà parvenu à un volume sensible, acquière des facettes additionnelles en continuant de s'accroître, s'il survient dans le fluide quelque changement qui détermine une nouvelle modification de forme " . Le cristal porte donc la trace de sa structure et de ses conditions de formation : Haüy renoue avec une tradition - l'influence, dans la cristallisation, de l'espèce et du lieu de la croissance - qui était sensible dans ses premiers travaux, mais qu'il distingue maintenant clairement. Il peut réaffirmer que la structure de la calcite résulte de l'empilement des molécules intégrantes rhomboédriques, mais peut préciser "il faut … que la diversité de formes secondaires … tienne à d'autres causes ; et il est tout simple d'attribuer ces causes aux circonstances extérieures, telles que les différentes densités du fluide … , la différence de ses températures, les divers mélanges … qui peuvent s'y rencontrer … . On conçoit que toutes ces circonstances, en faisant varier l'affinité du fluide à l'égard des molécules qui y sont suspendues, peuvent de même occasionner des diversités … au moment où il les abandonne. Le dernier effort de la Science serait de pouvoir soumettre toutes ces circonstances au calcul … . Mais nous sommes encore loin d'avoir toutes les données nécessaires pour résoudre ces sortes de problèmes "49. Belle limitation du sujet, beau programme de recherches, non encore épuisé actuellement.

En ce qui concerne la structure - à laquelle nous revenons - Haüy montre que la décroissance sur les bords d'un cube ne peut expliquer cristallographiquement l'existence d'un octaèdre (les " pas " des couches seraient incommensurables entre eux). Il faut donc admettre un autre type de décroissement : sur les sommets. Ce qui avait été annoncé dans l'Exposé abrégé… est maintenant démontré… et Haüy rejoint - en le généralisant - Romé de l'Isle ; il peut expliquer les cristallisations de la galène, de l'oligiste, dont la forme rhomboédrique est inscrite dans un cube.

Cet exemple donné est intéressant ; il montre combien, chez Haüy, la notion de symétrie est encore imprécise (il ne parviendra jamais à l'atteindre complètement) : si, en effet, un rhomboèdre peut être inscrit dans un cube, nous savons maintenant que la symétrie du cube et celle du rhomboèdre sont incompatibles entre elles et violent la " loi de symétrie " qu'Haüy lui-même énoncera en 1815, amenant ainsi à la fois unification et polémiques - nous y reviendrons. Pour l'instant Haüy intersecte mentalement tous les sommets, tous les angles, de ses molécules intégrantes par des plans différemment inclinés, conseille à ses auditeurs le " cours de géométrie descriptive donné par un de nos collègues " (Monge), déduit les formes secondaires engendrées, montre que quelquefois des figures régulières que présentent les cristaux (le prisme hexagonal de la calcite) sont dues à la combinaison de plusieurs formes secondaires particulières : dans tous les exemples qu'il prend, il montre une splendide virtuosité dans l'application de la géométrie dans l'espace et prouve qu'il possède parfaitement sa méthode, non encore sa théorie. Il note en effet : " Tantôt il y a uniformité entre tous les décroissements, de manière que c'est une seule loi … qui agit sur les différents bords, sur les différents angles … ; tantôt la loi de décroissement varie d'un bord à l'autre, ou d'un angle à l'autre " . Cette phrase cache encore une difficulté importante, nous y reviendrons là aussi.

Mais Haüy éprouve toujours un problème - qu'il ne parviendra jamais à résoudre entièrement : les " lames de clivages " qu'il détache des cristaux - il dira toujours partir de cette division mécanique, ce qui avait suscité l'ire de Romé de l'Isle - déterminent des angles plans qui se mesurent facilement. Mais on peut toujours - au moins en théorie - détacher une lame plus mince d'une lame précédemment définie. Quelle est donc la hauteur de la " molécule intégrante ", la valeur du troisième angle ? Haüy fait l'hypothèse que le rapport entre les trois angles soit tel que " les lois de décroissement soient les plus simples possibles " . Nous verrons que cette idée l'amènera à énoncer sa " loi des troncatures rationnelles ", loi construite, qu'il mettra en rapport avec la loi des proportions définies de Dalton, loi déduite de pesées, au statut épistémologique différent. Mais nous verrons aussi que ce parti-pris de simplicité dans la marche de la nature, fécond dans le cas de son "idée-mère " conduisant à l'idée de structure cristalline, masque aussi des imprécisions à la fois de mesures et de calculs. Nous n'en sommes pas là : pour l'instant Haüy soulève le problème à partir de la barytine, du gypse, le résout par la simplicité postulée des décroissements et conclut " Mais nous ne voudrions pas assurer que ce résultat fût général, parce que la force de l'adhérence peut ne pas dépendre uniquement de l'étendue des faces "55. Proposition qui semble devoir être admise par tous.

Les trois derniers exemples que nous venons de prendre en suivant Haüy montrent à quel point les cours de l'an III sont précieux : précieux pour les auditeurs qui voient se dévoiler devant eux la science la plus nouvelle et qui la comprennent grâce à l'art du pédagogue, précieux en ce qu'ils favorisent le développement et l'expression de la réflexion d'Haüy elle-même (il doit pour confronter ses propositions à la compréhension des étudiants exprimer la sienne propre, aborder et délimiter les problèmes sur lesquels il bute encore - ce que ne lui permettent de faire ni les ouvrages, ni les articles - précieux enfin pour l'historien qui possède un instantané irremplaçable de la maturation de la pensée d'un créateur en un instant donné. Un créateur qui n'hésite pas à faire rêver ses auditeurs sur les perspectives qu'ouvre la pratique de la science, sur les programmes de recherche qu'elle trace, sur l'œuvre à accomplir : " nos connaissances … se multiplieront avec rapidité … lorsque les Ecoles Normales, ayant propagé de toutes parts le goût de l'histoire naturelle et l'esprit d'observation, … , annonceront qu'au sein d'une patrie attentive à répandre parmi ses enfants le bienfait de l'enseignement, la nature elle même devient plus libérale de ses productions " . La structure détaillée, les formes primitives et secondaires expliquées par une même loi de décroissement, il ne reste plus à Haüy qu'à aborder le problème de la classification cristallographique. Il le fait dans la cinquième leçon, qu'il aborde encore à partir des " formes particulières, données par la division mécanique des cristaux " : même si Haüy, pour trouver les formes simples, le fait par la pensée quand les cristaux " ne se prêtent pas à cette division ", on va le sentir constamment bloqué par le recours aux clivages qui vont toujours chez lui empêcher à l'idéalisation mathématique d'atteindre sa parfaite étendue.

Comme dans l'Exposé abrégé…, Haüy distingue six formes primitives, que " l'analyse physique " permet - " par question de géométrie " - de réduire à " trois formes géométriques les plus simples ". Ce sont les " molécules intégrantes " de tous les cristaux. Là où Haüy disait dans l'Exposé abrégé ne pas vouloir se prononcer, il estime maintenant que cette idée est " plausible " : l'octaèdre se réduit au tétraèdre, voilà " où l'on reconnaît la marche ordinaire de la nature, et comme sa devise familière : économie et simplicité dans les moyens ; richesse et variété dans les effets ".

" Ces trois formes sont diversifiées dans les différentes espèces de minéraux, par des dimensions respectives et des mesures d'angles particulières. Par exemple, le parallélépipède est tantôt un cube ou un rhomboïde, et tantôt un solide, dont les faces ne sont pas semblables en elles. Le rhomboïde a ses angles au sommet plus ouverts dans le spath calcaire que dans le spath adamantin "53, ainsi de suite. Haüy nous entraîne dans un raisonnement, appuyé sur l'expérience, où il dit aussi que certaines formes de molécules sont communes à plusieurs substances : ce sont celles qui ont " un caractère particulier de régularité, et qui donnent des maximum ou des minimum de surface ou de solidité, tels que le cube, le tétraèdre " et que, toujours, le groupement des molécules intégrantes " qui sont les véritables molécules " permet, " en les prenant par petits groupes, d'en composer des parallélépipèdes ; et les lames de superposition décroissent par des rangées de ces parallélépipèdes ; en sorte que c'est à ce point de vue qu'il faut ramener le calcul dans la solution des problèmes " . " Ainsi … cette multitude de formes secondaires … dérive de six formes primitives qui … se réduisent à trois formes de molécules intégrantes … et ces trois dernières formes, considérées dans la manière dont elles obéissent à la loi des décroissements, rentrent dans une seule forme, qui est comme l'unité à laquelle se rapportent tous les résultats " .

Haüy tient l'unité cherchée, mais elle n'est qu'une unité liée à l'application de la loi de décroissement. Pourquoi donc garder trois molécules intégrantes différentes - le parallélépipède, le prisme triangulaire et le tétraèdre -, alors que la loi inférée et permettant de retrouver toutes les faces de tous les cristaux peut être appliquée grâce au recours aux seuls parallélépipèdes ? D'évidence Haüy est gêné par le fait que la division mécanique qu'il pratique sur certains cristaux parallélépipédiques peut donner des tétraèdres et des octaèdres (à partir d'un cube) et des prismes triangulaires (à partir d'un rhomboèdre). Géomètre, il dégage pour tous les cristaux - même ceux qui ne se clivent pas - le concept de molécule intégrante, une structure unique, une seule loi de décroissement, mais il reste trop physicien et s'arrête à ce que lui révèle " l'analyse physique " c'est-à-dire le groupement, réel pour lui car physique, de molécules intégrantes qui remplissent l'espace, même si l'analyse chimique permet de séparer les éléments ou des groupements de matière qui ne remplissent pas l'espace. La molécule intégrante possède donc une existence physique tandis que le parallélépipède unique, " remarquable par sa simplicité ", et qui est " comme l'unité à laquelle se rapportent tous les résultats ", peut être produit par " de petits groupes " de molécules intégrantes : il est une sur-structure géométrique, non la manière dont le Créateur a procédé.

Haüy termine la partie de son cours portant sur la cristallographie en donnant " une idée de la méthode de calcul " qu'il a utilisée. C'est un beau sujet de méditation pour qui veut se poser le problème épistémologique de la méthode expérimentale et des relations qu'entretient l'expérimentation avec les conceptualisation, théorisation, mathématisation. Haüy nous dit être parti " dans les premiers essais de la théorie " de " méthodes particulières pour vérifier l'existence de la loi des décroissements ". Celle-ci n'était pas établie, Haüy en avait l'intuition, confirmée " par de simples calculs trigonométriques. Mais lorsque la théorie eut fait un certain progrès, on s'occupa de ramener le calcul à un petit nombre de formules générales " par la recherche d'une simplicité postulée, simplicité " d'où l'on pût toujours partir pour arriver, par une marche courte et directe, à ces mêmes résultats … On avait même alors, relativement à la théorie dont il s'agit, l'avantage de déterminer facilement toutes les formes possibles, et d'anticiper sur les découvertes à venir. C'était une manière de pénétrer, à l'aide du calcul, dans les retraites de la nature, et d'en faire sortir d'avance les productions qu'elle dérobait encore à nos regards " . Alors, grâce à la théorie, "assez souvent l'œil devine d'avance … et dispense du tâtonnement ", le calcul confirme et permet de trancher entre quelques solutions possibles.

Et Haüy de conclure : " Il reste de grands pas à faire pour terminer la théorie de la cristallisation : nous n'avons donné que les lois de la structures des cristaux, et il faudrait pouvoir trouver celles de leur formation … les données nous manquent encore . Les solutions des problèmes " sont réservées à d'autres temps et à d'autres moyens … . C'est ici une mine féconde, dont l'exploitation est seulement commencée, et qui attend des mains plus savantes pour en suivre la veine à une plus grande profondeur " .

Le Traité de minéralogie est le grand œuvre d'Haüy et - même si, sur de bien des points celui-ci va en corriger et développer plus tard certaines propositions -, on y sent l'aboutissement des efforts d'un homme dont la théorie est arrivée à maturité : ses observations nombreuses et patientes, ses modélisations, les discussions et confrontations qu'il a menées, les rédactions d'articles et d'ouvrages, ses enseignements aux savants réunis dans la chambrette et aux élèves de l'Ecole normale de l'an III aboutissent à des propositions simples et cohérentes.

Haüy se propose dans le Traité de décrire les propriétés de tous les minéraux et de les classer. La physique, la chimie et la géométrie contribuent ensemble à permettre l'analyse minéralogique ; les modes de distribution et d'études auxquels ces trois sciences sont habituées n'ont pas de ligne de démarcation nette : elles doivent " se prêter la main … et marcher … sur une même ligne c'est à la chimie qu'il appartient la détermination des espèces " mais " que la géométrie … soit associé à la balance " pour rapprocher " tous les minéraux connus sous un même point de vue, pour les comparer entre eux, étudier leurs caractères, et interroger tour à tour l'expérience et la théorie sur les différents phénomènes dont ils sont susceptibles ". Nous sommes loin de l'affirmation contenue dans l'Essai… : " jamais on ne pourra faire de la cristallographie la base d'une distribution méthodique des minéraux ".

Une classification doit permettre de déterminer un minéral et de donner la série de ses variétés. Il faut donc trouver premièrement la composition chimique qui donne l'espèce, puis la molécule intégrante qui donne le type de l'espèce (la calcite et l'aragonite, qui ont même composition, ont des formes cristallines différentes et ne sont pas les même minéraux). Ce type de l'espèce peut encore être appelé " espèce minéralogique " qui est " une collection de corps dont les molécules intégrantes sont semblables, et composées des mêmes éléments unis en même proportion " . On peut alors pour chaque espèce minéralogique déterminer les caractères spécifiques mesurables : pesanteur spécifique, dureté, réfraction double ou simple, électricité, phosphorescence… (sont donc exclues les propriétés comme les couleurs), puis les formes présentées par les différentes variétés, avec les valeurs de leurs angles, les noms qu'on leur attribue, enfin des " annotations qui … renferment comme l'histoire " des minéraux : gisements, associations. C'est donc un panorama précis de l'ensemble du règne minéral connu à son époque que va tracer Haüy en proposant une classification nouvelle et des nomenclatures rationnelles des espèces et des formes.

Mais il lui faut commencer par préparer le lecteur à l'étude cristallographique. Haüy va le faire de deux manières : " l'une par le simple raisonnement aidé de figures qui rendent sensibles à l'œil le mécanisme de cette structure, l'autre, dans un article séparé, à l'aide de l'analyse mathématique, en donnant aux résultats toute la généralité que comporte le sujet " .

La première manière est développée grâce au travail de plusieurs collaborateurs qu'il cite : Haüy offre au lecteur des planches splendides utilisant les méthodes de projection de Monge et illustrant la théorie physique des couches de décroissement, qu'il fait parfaitement comprendre notamment à partir du rhombododécaèdre et du scalénoèdre de calcite (Fig. 4) - il n'y a pas ici d'innovation par rapport aux cours de l'an III, sinon une meilleure démonstrativité des figures.

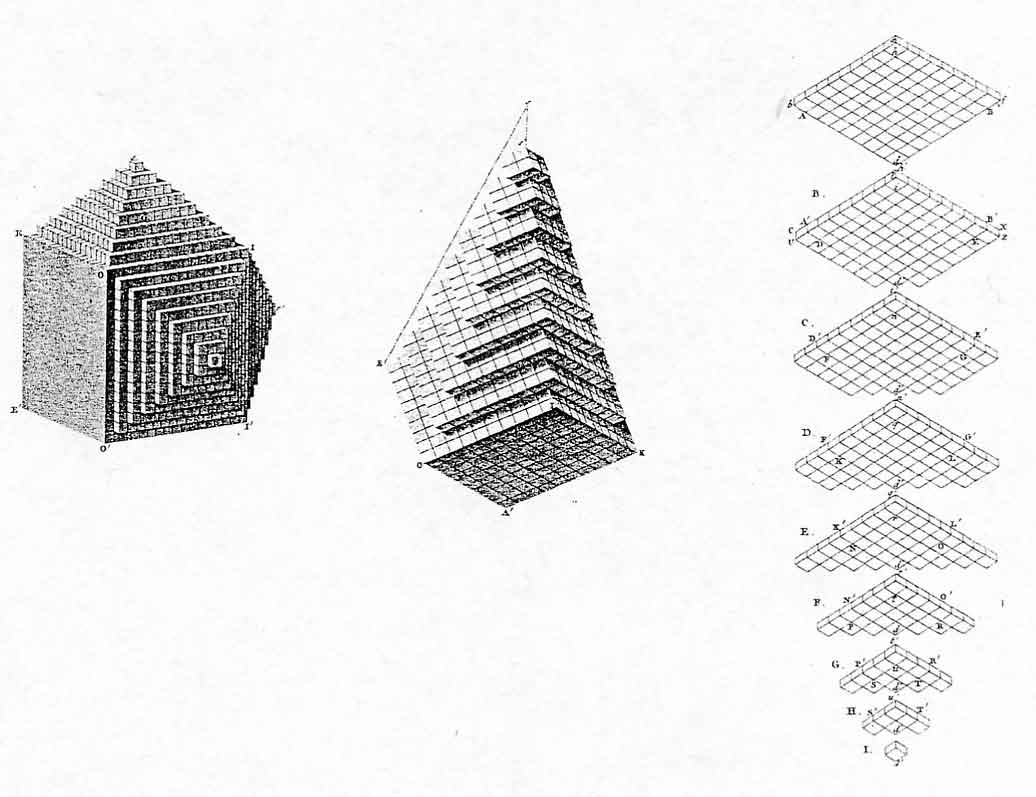
Figure 4. Les couches de décroissement conduisent à la cristallisation du rhombododécaèdre de pyrite et au scalénoèdre de calcite (Haüy : Traité de minéralogie).

Par la seconde méthode, Haüy montre comment la géométrie permet de prévoir et de nommer les formes secondaires une fois la molécule intégrante et le parallélépipède de base déterminés : il part de celui-ci et, par troncatures successives sur les bords et les sommets, montre que l'on retrouve les formes. Ici Haüy reprend encore, mais détaille précisément ce qu'il avait esquissé lors des cours de l'an III. Nous allons y revenir.

Il reste à bien préciser ce dont on parle, puisque chimie, physique et géométrie vont être mêlées. C'est ce que fait Haüy dans une introduction qui lui permet de préciser encore sa réflexion. Dans les corps, il y a deux ordres de molécules : les premières, " les molécules élémentaires " sont les composés chimiques combinés selon un arrangement déterminé dans le minéral (par exemple l'acide et la soude dans le sel commun) ; elles sont accessibles grâce à l'analyse chimique qui en donne la proportion. Les secondes, " les molécules intégrantes ", sont les plus petits volumes du corps pouvant être obtenus sans que sa nature soit détruite ; elles sont accessibles par l'analyse cristallographique qui en donne la forme. " Les molécules élémentaires ont sans doute aussi des formes régulières et constantes pour chaque espèce d'acide, d'alkali, etc ; et celles d'une espèce s'adaptent à celles de l'autre, en formant de petits compartiments d'où résultent les molécules intégrantes " ajoute Haüy.

Après avoir détaillé les propriétés chimiques et physiques qu'il va utiliser, les méthodes de mesures adoptées, Haüy peut constituer de très utiles tables de détermination qui réforment celles qu'avait établies avant lui Romé de l'Isle, et passer à l'étude de la " partie géométrique ". Celle-ci lui permet de développer somptueusement son " analyse mathématique des cristaux ". Un cristal est toujours constitué par l'une des six formes possibles de " formes primitives ", qui se réduisent à trois formes possibles de " molécules intégrantes ". Celles-ci sont des parallélépipèdes ou peuvent s'y ramener en se groupant. Ces parallélépipèdes seront appelés " molécules soustractives ". C'est une " espèce d'unité à laquelle on peut ramener la structure de tous les cristaux en général, en sorte que l'on est libre de s'en tenir aux données qu'elle fournit, dans l'application du calcul à toutes les formes cristallines possibles " .

En partant de cette idéalité que constituent les parallélépipèdes, Haüy peut les supposer intersectés sur les bords, sur les sommets ou de manière intermédiaire, figurer ainsi les décroissements qui conduisent à la formation des faces, donner les formes secondaires qui en résultent, en préciser les angles, les nommer. Haüy ne peut mener ce travail qu'après avoir lui-même visualisé par la pensée toutes les conséquences des lois de décroissement, y amenant ensuite le lecteur pas à pas au moyen du raisonnement géométrique et de sa traduction analytique. En deux cent quarante pages d'études serrées, faisant appel à de nombreuses démonstrations de trigonométrie plane, Haüy développe ses idées. Il va devenir, dira Cuvier [Eloge ..., op.cit.], le " législateur de la minéralogie ", un législateur dont les raisonnements ne pourront plus être suivis par les naturalistes de son époque, mais passionneront physiciens et géomètres. Cuvier qualifie ainsi le traité : " Ce livre a en effet au plus haut degré deux avantages : le premier, qu'il est fondé sur une découverte originale ce qui est faux ; la seconde, que cette découverte y est suivie et appliquée avec une persévérance inouïe aux moindres variétés minérales. Tout y est grand dans le plan, tout y est précis et rigoureux dans les détails ; il est fini comme la doctrine même dont il contient l'exposition " .

Nous ne pouvons dans le cadre de cette étude détailler même la seule partie cristallographique du " Traité de minéralogie " (dont trois tomes sont en outre consacrés à la description des minéraux particuliers). Nous préférons nous appuyer sur l'ouvrage et ceux qui l'ont suivi pour montrer la beauté de la doctrine, mais aussi qu'elle n'était point encore finie : elle va encore être améliorée par Haüy, contestée également dans ses détails et ses fondements du vivant même de celui-ci.

La classification donnée dans le Traité de minéralogie est chimique en ce qui concerne la détermination des " espèces ", et cristallographique pour les " types de l'espèce " ou " espèces minéralogiques ". Or, l'époque est celle d'un conflit entre des chimistes (comme Proust) qui affirment que la composition chimique des composés particuliers est constante et d'autres qui, avec Berthollet, pensent que - à l'image des gaz et des liquides - la composition des composés solides peut varier et dépend d'un équilibre dynamique entre les constituants au moment de la cristallisation. A ce débat viennent bientôt s'ajouter les critiques de tous ceux - dont Berthollet - qui remarquent que Haüy donne pour des espèces minérales des compositions chimiques qui ne peuvent être celles de leurs molécules intégrantes… Or les molécules intégrantes sont censées représenter des petites masses qui ont, intégralement, les propriétés chimiques et physiques des cristaux… Haüy reprend donc ses études. Il reconnaît le bien-fondé de cette dernière critique. Il est amené à proposer [René-Just Haüy, Tableau comparatif des résultats de la Cristallographie et de l'analyse chimique, relativement à la classification des Minéraux, Paris, 1809] qu'une molécule intégrante particulière possède une composition chimique particulière parmi d'autres possibles, mais que plusieurs compositions sont représentées dans un même cristal. Cette variation agit certainement sur les formes extérieures des minéraux. De " principes accidentels " dépendent donc la composition chimique, la dureté, la couleur, la densité, les formes extérieures, mais la géométrie de la molécule intégrante est constante : " il n'y a que la Géométrie pour laquelle tous les minéraux soient purs " écrit-il .

Dès lors, Haüy va penser à modifier son système de classification. Dans son dernier ouvrage, le Traité de Cristallographie, qu'il tiendra dans ses mains avant sa mort (1822), il change radicalement de position et déclare dès l'introduction " Je prouve … que c'est à la Cristallographie plutôt qu'à la chimie qu'appartient la distinction des espèces, et je me fonde principalement sur ce que la condition essentielle, qui exige que l'espèce soit représentée, ne peut être remplie que par celle des deux sciences qui nous dépeint les minéraux tels que les a produits la nature, et non celle qui ne nous les fait connaître qu'à l'aide d'une opération dont les résultats ont effacé leurs traits caractéristiques " [René-Just Haüy, Traité de Cristallographie, Paris, 1822].

Des " lames de décroissements " des premières études, aux couches de " molécules soustractives " enlevées - par pure opération géométrique - aux sommets et aux bords des parallélépipèdes pour retrouver les formes secondaires, la pensée de Haüy a évolué. Puisque les couches ont toujours une hauteur égale à un nombre entier de celle d'un parallélépipède, puisque les lois des décroissements sont supposées les plus simples possibles, Haüy peut aller plus loin dans l'exploitation de l'idée-mère que lui a donnée le clivage de la calcite. Dans le Traité de 1802, il énonce clairement ce qui sera appelé " loi des décroissements rationnels " : les troncatures des parallélépipèdes ont une inclinaison toujours mesurée par des rapports rationnels.

Mais l'année même où est publié le Traité de Minéralogie (1802), en Angleterre Thomas Young soutient une théorie ondulatoire de la lumière, découvre les interférences, revient aux explications de la réflexion et de la réfraction qu'a données Christiaan Huygens en 1678 (lecture à l'Académie des sciences) et 1690 (Traité de la lumière), tandis qu'un autre anglais, Wollaston, s'avise que le grand Newton, avait, dans son Optique de 1710, détruit la théorie de Huygens en disant que les mesures faites des angles de la calcite et de la double réfraction sont fausses. Il reprend ces mesures, et à sa grande stupéfaction, voit que Huygens avait raison : les inclinaisons des faces de la calcite sont de 45°23 par rapport à la verticale (Huygens donnait 45°20, Haüy donne 45°) et de 105°5' pour les angles dièdres (Huygens donnait 105°, Haüy donne 104°28).

Wollaston veut préciser son travail, vérifier par une autre méthode ses résultats fondamentaux. Il invente un " goniomètre à réflexion " grâce auquel la mesure des angles se fait par réflexions successives d'un pinceau lumineux sur les faces d'un cristal, et non plus par application de réglettes se déplaçant devant un rapporteur. La précision qu'il atteint est de l'ordre de 2' (Haüy avec son goniomètre d'application évalue ses erreurs à 20'), ce qui permet à Wollaston de confirmer ses résultats. Le monde scientifique est incrédule. En France, l'Institut demande à Haüy de dire qui de Newton ou de Huygens a raison. Haüy désigne celui-ci. L'Institut annonce (janvier 1808) qu'il attribuera un prix à qui donnera " de la double réfraction que subit la lumière en traversant diverses substances cristallisées, une théorie mathématique vérifiée par l'expérience ". C'est Malus [Etienne Louis Malus, Théorie de la double réfraction de la lumière. Mémoire couronné par l'Institut, Paris, Baudouin, 1810, p. 291] qui obtiendra ce prix, confirmant les mesures de Wollaston grâce à l'invention d'un autre appareil de mesure, le " cercle répétiteur ". Mais surtout, grâce à cette étude, il découvre la " polarisation " par réflexion de la lumière (1810).

Il est maintenant évident aux yeux de tous que les valeurs que donne Haüy de l'inclinaison des faces du spath d'Islande sont fausses à 32' d'angle près, alors que la précision de son appareil est de 20'. Ce problème est grave puisque c'est justement à partir de la division de la calcite qu'Haüy a bâti sa théorie. Il va s'ensuivre une polémique dans laquelle, pour sauver la simplicité de sa théorie, Haüy dit refuser d'utiliser le goniomètre de Wollaston (il finira par utiliser le cercle répétiteur). Pour justifier sa position, il affirme que les imperfections des faces naturelles sont telles qu'il est inutile de vouloir obtenir une grande précision de mesure. Dans deux articles de 1811 [René-Just Haüy, Observations sur la simplicité des lois auxquelles est soumise la structure des cristaux, Ann. Mus. Hist. Nat., XVIII, 1811] et de 1818 [René-Just Haüy, ibid., Observations sur la mesure des angles des cristaux, Journ. de Phys., 87, 1818, p. 243-244 et 249] il change de tactique et énonce clairement que les valeurs d'angles qu'il donne sont telles que les couches de décroissement sont également inclinées sur la base et la hauteur (45°) et forment à l'intérieur d'une couche des rapports simples 3/2 donc 104°28 et non 111/74 soit 105°5 " le cristallographe qui a calculé un de ces angles liés étroitement à ce résultat fondamental, ne le mesure ensuite que pour se satisfaire. Il ne doutait pas d'avance que l'observation, si elle était exacte, ne dût parler comme la théorie " et encore : " la méthode que j'avais adoptée … semblait me dispenser d'une plus grande précision, parce qu'elle me fournissait un moyen de reconnaître, à l'aide de la théorie, le terme où je devais m'arrêter, au milieu des variations que subissaient mes résultats ". Haüy désigne ce terme théorique sous le nom de " limite " et montre qu'il détermine celle-ci en recherchant par le calcul des rapports simples. " La méthode que j'ai adoptée pour obtenir ces rapports sous la forme la plus avantageuse, consiste à représenter, par des quantités radicales les deux termes qui les composent ".

Haüy croit renforcer encore sa position en montrant (1811) que sa loi des décroissements rationnels est à mettre en relation avec le " principe des proportions définies " que vient d'énoncer (1803) le chimiste Dalton, et contre lequel s'élève Berthollet. Dalton, grâce à des pesées, montre que les masses des éléments chimiques qui se combinent dans un corps sont toujours entre elles dans un rapport simple. Ne sont-ce pas aussi des rapports simples que font entre eux les pas des couches de décroissance ? La nature procède toujours avec simplicité. Et, dans le Traité de Cristallographie, Haüy de déclarer " J'avais aperçu depuis longtemps la liaison de ce principe de simplicité avec la géométrie des cristaux et elle m'avait servi à en démontrer l'existence ". Mais les rapport simples pourraient être plus proches des mesures de Huygens, Wollaston, Malus, Biot… si Haüy utilisait la trigonométrie sphérique. Autodidacte en mathématiques, il adopte toujours - ce que personne ne remarque - la trigonométrie plane, et prend comme solides de référence, comme modèles, ceux où elle s'applique avec le plus de précision.

Dans le Traité de Cristallographie de 1822, Haüy soutient encore sa position au moyen d'un principe bien intéressant du point de vue épistémologique : " les mesures mécaniques des angles que font entre elles les faces … ne peuvent être rigoureuses … les rapports qui en dérivent … seront représentés par de grands nombres, dont l'usage nuira à l'élégance de la théorie et la rendra moins maniable. Je fais voir comment je suis arrivé à déduire de ces rapports approximatifs et compliqués, une limite qui se reconnaît à sa simplicité et dans laquelle réside très probablement le véritable rapport, qui est celui de la nature " . Dans cette conception des rapports qu'entretiennent théorie et expériences, nous sommes loin des principes développés par Haüy dans ses cours de l'an III. Maintenant, en ce qui concerne tous les cristaux, Haüy écrit : " J'étais donc conduit par l'analogie à conserver, autant qu'il était possible, le même mode d'expression à l'égard des rapports entre les dimensions des formes, qui n'ont pas le caractère de limite. Un autre avantage joint à celui de l'uniformité qui en résulte, est de faciliter et de simplifier les calculs " , position qui peut être généralisée à l'ensemble de la pratique scientifique puisque " il en était de ces deux inclinaisons égales des faces du rhomboïde sur un plan horizontal et un plan vertical, comme des durées des deux moyens mouvements de rotation et de révolution de la Lune, dont l'égalité, regardée comme absolue par les géomètres et par les astronomes, sert comme de point fixe dans les calculs relatifs à l'Astronomie " .

Le réel ne peut être appréhendé sans idées préconçues qui s'efforcent de le rendre intelligible : Haüy plie ici l'expérience aux exigences de la théorie. Position qu'il avait justifiée dans l'introduction générale de son Traité de Cristallographie : " On reconnaît ici ce qui caractérise en général les lois émanées de la puissance et de la sagesse du Dieu qui l'a créée et qui la dirige. Economie et simplicité dans les moyens, richesse et fécondité inépuisable dans les résultats " . Des phrases analogues reviennent sans cesse, nous l'avons vu, sous la plume d'Haüy et constituent sa conviction profonde. Mais cet assujettissement de l'expérience n'est guère apprécié - nous le verrons - de ses contemporains, surtout des étrangers, et n'est pas sans tourmenter Haüy lui-même, ainsi que le rapporte Cuvier : " Il se concentrait entièrement " à sa théorie sur la matière ; ce n'était qu'avec impatience qu'il s'en voyait détourné par des objections ; son repos en était troublé ; c'était le seul motif qui pût le faire renoncer à sa douceur … ordinaire … . Cette disposition … l'a peut-être empêché d'avoir assez d'égards aux observations … de M. Wollasto [sic] … . Mais qui n'excuserait un homme valétudinaire … de n'avoir pas assez distingué de ses premiers et ignorants antagonistes [Cuvier vise ici Romé de l'Isle] ceux qui, … éclairés par ses propres découvertes, apprécièrent autrement que lui … quelques principes qu'il avait trop généralisés ? Ce qui est certain, c'est que dans les moments où il payait ce tribut à la faiblesse humaine, il n'était animé que de ce qu'il croyait l'intérêt de la science " .

Haüy va trouver une occasion de s'approcher par d'autres voies de la perfection souhaitée. Dans le Traité de 1801, il avait classé les minéraux selon leurs parallélépipèdes soustractifs (qu'il ne dénombre pas), et avait proposé une notation des faces en fonction des troncatures opérées par la pensée sur les sommets et sur les bords.

Généralisant cette méthode de notation aux faces de tous les minéraux qu'il connaît, il en arrive à proposer en 1815 sa " loi de symétrie " qui systématise les conclusions déjà tirées sur l'inclinaison des couches de décroissement et permet de déduire toutes les faces de toutes les formes de tous les cristaux : " si le bord d'un parallélépipède primitif subit un certain décroissement ou reste identique à lui même, les autres bords analogues subiront le même décroissement ou resteront identiques. Il en est de même pour les angles " [René-Just Haüy, Mémoire sur une loi de cristallisation appelée loi de symétrie, Mém. Mus. Hist. nat., I, 1815, p. 81-101]. Mais, dès 1815, Haüy admet qu'il y a quelques exceptions à sa loi : certaines formes que présente la cobaltine - des tétraèdres - peuvent se déduire d'un cube par décroissement d'un sommet sur deux seulement ; certains cristaux dodécaédriques de la pyrite - ceux- là même qu'Haüy avait opposés à Romé de l'Isle - peuvent se retrouver à partir du décroissement d'une arête sur deux d'un cube… et le rhomboèdre inscrit dans un cube ne peut se déduire de celui-ci : Haüy reconnaît cette erreur. S'appuyant sur le fait que la cause de la cristallisation est inconnue, il justifie ces " merveilleuses exceptions ", rares, par des circonstances particulières qui auraient dévié la cristallisation du chemin qu'elle devrait suivre si elle était laissée à elle-même. Ce sont ces mêmes circonstances qui produisent - pense-t-il - la pyroélectricité de la tourmaline : ses différentes parties constitutives auraient leurs configurations altérées.

Mais n'est-ce pas un défaut de la théorie d'Haüy que révèlent toutes ces exceptions ? Celles relatives à la " loi de symétrie ", celles à la " loi de décroissement rationnel ", ces mesures qui ne rendent pas compte des prévisions de la théorie ? C'est ce que pense un cristallographe allemand, Weiss, qui traduit dès 1804 le Traité de minéralogie. Il avait séjourné en France en 1802, rencontré Haüy qui l'avait accueilli aimablement (le 7 mai) et lui avait donné l'autorisation de regarder sa collection. Mais au cours d'un autre séjour, en 1807, Weiss suggère à Haüy une autre théorie que la sienne. Celui-ci ne peut supporter que son mérite ne soit pas reconnu tout entier : il saisit Weiss au collet [Websky et al., cité par John G. Burke, Origins of the Science of Crystals, Berkeley and Los Angeles, 1966, p. 154] … nouveau tribut payé à la faiblesse humaine ? C'est donc en Allemagne, et en France seulement après la mort du " despote " Haüy que va être modifiée la théorie cristallographique. Nous ne ferons qu'évoquer très brièvement ces efforts en ce qu'ils prolongent et réforment les intuitions d'Haüy en donnant tout le caractère de généralité souhaitable aux " réseaux cristallins ", préparant ainsi nos modernes théories.

En publiant en 1804 la traduction allemande du Traité de Minéralogie, Christian Samuel Weiss y ajouta un long paragraphe attaquant " la théorie atomistique " et lui préférant la théorie dynamique de la matière de Kant [Christian-Samuel Weiss, Dynamische Ansicht der Kristallisation, in Der Bürger Haüy, Lehrbuch der Mineralogie... Leipzig, 1804, p. 365-389]. Sans entrer dans les détails, disons qu'à la suite de Leibniz, Boscovich et Kant, s'était affirmée en Allemagne, dans le mouvement de la " Naturphilosophie ", une tradition beaucoup plus conceptuelle, théorique et abstraite de la matière, faisant de celle-ci un continuum divisible à l'infini au sein duquel peuvent agir des forces attractives ou répulsives, exercées en des points purement mathématiques. La cohésion de la matière devient alors le résultat de l'équilibre dynamique de l'action de ces forces : quand la distance dépasse une certaine limite, la force est attractive, elle devient répulsive en deçà. Pour Boscovich (1780) ces forces ne sont pas isotropes lors de la cristallisation, des faces apparaissent. Friedrich Schelling (1804) conclut à partir de la considération de la mécanique et de la statique de son temps que chaque phénomène peut être représenté de manière panthéiste et dérive idéalement de l'Absolu. Il y a dans la nature, pense-t-il, un pouvoir universel de formation qui produit les choses individuelles avec des rôles déterminés : tels les cristaux, constitués de matière et de forme. La cristallisation obéit à un principe positif : réaliser la forme. Les différences observées dans les cristaux tiennent à l'action d'un principe négatif qu'il faut chercher, et " c'est un jeu habile auquel se livre Haüy - note Schelling - lorsqu'il regarde toutes les cristallisations comme produites par différentes agrégations de formes primitives inaltérables " [Friedrich von Schelling : Von der Weltsek, Hamburg, 1798, p. 227 cité par G. Burke, Origins..., op. cit., p. 15].

Ce sont ces idées théoriques que Weiss reprend et étend : pour lui, les forces attractives et répulsives sont en équilibre dans un fluide. La cristallisation se produit lorsque les forces répulsives deviennent dominantes. Comme elles ne sont pas isotropes, des faces apparaissent perpendiculairement aux forces. Ce sont donc des directions qui sont caractéristiques d'un cristal ; ce sont les répétitions de directions concourantes et identiques qu'il faut étudier. Pour ce faire, Weiss introduit le concept " d'axe de symétrie " qu'avait suggéré en son temps Christiaan Huygens. Ainsi peut-il donner de la cristallisation une représentation que nous qualifierions aujourd'hui de vectorielle, l'applique, comme Huygens, à la calcite, montre que, dans le cas général, la considération d'axes de symétrie n'est pas seulement géométrique, mais possède une signification physique : les faces, les clivages, les valeurs de la biréfringence… se répètent selon ces axes. Continuant et systématisant ses efforts sur les minéraux connus, Weiss propose en 1815 [Christian-Samuel Weiss, Ubersichtliche Darstellung..., A.D.B., 1814-1815, p. 289-364] une classification dans laquelle il place les minéraux en fonction des axes qu'ils possèdent. Il distingue sept systèmes différents caractérisés par les systèmes d'axes que comportent les différents types de parallélépipèdes : le cube est le seul parallélépipède qui ait trois axes principaux, à angles droits ; trois autres systèmes ont un seul axe principal (nous dirions, tétragonal, rhomboédrique, hexagonal) ; trois autres (appelés aujourd'hui orthorhombique, monoclinique, triclinique) ont trois axes non principaux perpendiculaires (Weiss se trompe en cela sur les deux derniers systèmes). Weiss peut alors calculer pour chaque système ce que nous appelons le degré de symétrie, utilise pour rapporter les faces aux axes la trigonométrie sphérique, démontre que, pour la calcite, Haüy s'est trompé en prenant comme élément caractéristique fondamental les diagonales des faces et non les axes - ce qui explique en partie la non-concordance de sa théorie avec les mesures -, rapporte toutes les faces des formes secondaires aux axes sans qu'il soit besoin de faire appel aux molécules soustractives, démontre que deux des " molécules intégrantes " de Haüy - le tétraèdre et le prisme triangulaire - se rapportent à un parallélépipède, montre que certaines symétries sont " hémièdres " ou " tétartoèdres ", et constituent ainsi des " sous-systèmes ". Beaucoup d'aspects modernes de la cristallographie sont ainsi présentés pour la première fois. Mais Weiss ne fait pas seulement de la cristallographie une stricte science géométrique - ce qu'Haüy n'avait pas réussi - : en traitant mathématiquement les variables caractéristiques de chaque propriété physique, en donnant une notation des faces selon les intersections qu'elle déterminent avec les axes, il fait aussi œuvre de physicien. Une œuvre qui sera très bien reçue en Allemagne puis, pour la systématisation qu'elle permet, en Angleterre où Miller, par simplicité, donnera une notation des faces par trois nombres entiers et premiers entre eux, inverses des rapports d'intersections déterminés par Weiss.

Mohs (1822) corrigera les erreurs de Weiss concernant les deux systèmes les moins symétriques tandis qu'il appartiendra à Johann Hessel de parfaire le travail. Hessel combine (1830) tous les axes de symétrie concourants compatibles avec les polyèdres cristallins, distingue axes directs et axes inverses, dénombre [J.F.C. Hessel, Kristallometrie oder Krystallonormie und Kristallographie, Leipzig, 1897] trente-deux classes de symétries réparties en sept systèmes. Le dénombrement complet des classes de symétrie est effectué. Hessel peut y ranger tous les minéraux connus. Il reste des classes vides : ce sera le travail des minéralogistes de les combler ultérieurement. Mais les travaux de Hessel resteront méconnus pendant soixante dix ans, même en Allemagne.

En France, la réaction est vive contre les déductions des cristallographes allemands. Delafosse et Durozier écrivent dans un article sur Haüy " Nous devons toutefois reconnaître que la théorie de Haüy s'attire une défaveur presque générale en Allemagne. Les minéralogistes de ce pays, en acceptant … les bases des idées d'Haüy en rejettent complètement la forme. Il est nécessaire de rechercher la cause de l'antipathie que ces savants d'outre-Rhin ont manifestée pour la théorie moléculaire dans la philosophie idéaliste : ce type de considération métaphysique qui préoccupe tous les intellectuels allemands. Quelques équivoques reprises des grecs, quelques sophismes basés sur les fameuses antinomies de Kant, ont conduit les physiciens allemands à préférer dans l'étude et l'interprétation des phénomènes naturels les sortes de vagues et obscures explications qu'ils appellent " dynamiques " plutôt que des simples, claires et positives notions que nous tirons des hypothèses atomistes … Les deux lois fondamentales … d'Haüy … sont présentées comme de simples lois empiriques ; elles ont perdu le caractère de lois a-priori, ce qui les distingue de la théorie qu'Haüy nous donne " [G. Delafosse et R. Durozier, René-Just Haüy, in Biographie universelle, Michaud, 1850]. De telles positions empêchent les savants français de considérer sans passion les résultats des cristallographes allemands. C'est donc en ignorant à peu près totalement les résultats que nous venons de mentionner que l'œuvre d'Haüy est poursuivie en France, dans le but d'en résoudre les contradictions.

Gabriel Delafosse, un élève d'Haüy, regrette en 1840, bien longtemps donc après la mort de son maître, que celui-ci ait " délaissé toutes les propriétés autres que le clivage " et n'ait pas " donné à ses travaux le caractère d'une théorie physique " [Delafosse, Recherches relatives à la cristallisation considérée sous les rapports physiques et mathématiques, Paris, 1840]. Voulant rendre compte notamment des hémièdries, il remarque que les cristaux " géométriquement semblables peuvent répondre à des structures moléculaires différentes ". Puisque celles-ci ne remplissent pas l'espace, la structure cristalline est formée par des " polyèdres atomiques " disposés aux " nœuds " d'un réseau tripériodique de points virtuels définissant des " rangées réticulaires ". Celles-ci délimitent des parallélépipèdes, les " mailles ", pouvant être mises en correspondance avec les sept systèmes cristallins (les primitifs). Mais les polyèdres atomiques n'ont pas obligatoirement les mêmes symétries que les mailles : elles peuvent n'être " physiquement identiques qu'à la moitié ou au quart des primitifs " (Fig. 5), " les lignes de réseau restant les mêmes ". Par cette remarque, Delafosse donne une explication fondée sur l'hypothèse moléculaire des hémiédries. Pour lui, les systèmes cristallins " se divisent quand on considère les modifications physiques que peut entraîner un changement dans la forme ou la structure des cristaux ". Trop physicien, il n'entreprend pas l'étude de toutes les subdivisions possibles : il décrit et classe ceux des cristaux et celles des propriétés que l'expérience lui fait connaître.

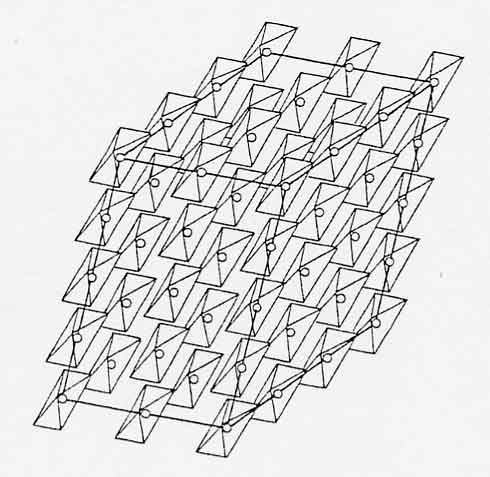
Figure 5. Les " polyèdres atomiques " de Gabriel Delafosse (1840).

Les notions de motif atomique, de réseau réticulaire, de mailles introduites par Delafosse, vont être généralisées en 1848 par les travaux exclusivement géométriques d'Auguste Bravais [Auguste Bravais, Les systèmes formés par des points, Journ. de l'Ecole polytechnique, XX, 1850]. Celui-ci réduit les molécules polyédriques ne remplissant pas l'espace à de simples points et se livre à un travail mathématique consistant à étudier les réseaux de translations à une, deux ou trois dimensions. Il introduit les notions de " mailles simples " (elles ont un seul nœud propre) et de " mailles multiples ", en calcule surfaces et volumes. Il peut alors dénombrer cinq modes de réseaux bidimensionnels et quatorze modes de réseaux tridimensionnels qu'il range dans les sept systèmes. Ce travail, Bravais veut le limiter " à la pure spéculation géométrique " et le préserver ainsi des risques qu'il peut faire courir à son œuvre en la liant à la spéculation mécanique, voire atomiste. C'est qu'en 1848, l'atomisme recule : la physique de Newton-Laplace vient d'essuyer une série de revers cuisants en optique, en électricité, en magnétisme, dans la théorie de la chaleur… et Bravais se risque simplement à écrire à la fin de son mémoire " l'observation des corps cristallisés … prouve a-posteriori … ce que révèle mon étude théorique ".

Il restera à la cristallographie de la sphère allemande à unifier les études et parfaire l'œuvre de dénombrement : Sohncke (1879) introduit des axes hélicoïdaux et - ne connaissant pas les travaux de Hessel - dénombre soixante et un groupes d'espaces, tandis qu'en 1885, Arthur Schöenflies et le russe Fedorov se posent, indépendamment l'un de l'autre, le problème de la partition régulière de l'espace, de manière générale, sans figure. Ils ne trouvent la solution qu'en 1891 en introduisant dans les réseaux des éléments de symétrie non concourants. Ils dénombrent deux cent trente sous-groupes.

En 1897, Schöenflies va plus loin et propose une classification complète : il subdivise les sept systèmes en trente deux classes, affecte à chacune de celles-ci les " réseaux de Bravais " compatibles, y place les " sous-groupes " correspondants.

Avec Schöenflies et Fedorov, avec surtout la magistrale synthèse de Pierre et Jacques Curie (1894), la symétrie perd sa forme, ne s'applique plus à l'étude des formes et propriétés, mais devient outil de raisonnement, un peu comme chez Archimède la balance permet la naissance d'un raisonnement dans lequel la forme s'est inscrite mentalement et produit des idées.

Le travail commencé par Romé de l'Isle et René-Just Haüy trouve alors son achèvement. Il faudra attendre l'expérience de Max von Laüe (1922) pour que l'hypothèse réticulaire bénéficie d'une confirmation expérimentale… et attendre aussi les travaux des Bragg père et fils, après 1930, pour que la notion de groupe rencontre une utilité pratique dans la détermination des structures cristallines.

Avec la symétrie, une structure unique décrit alors un ensemble de phénomènes variés, qui semblaient totalement étrangers les uns aux autres. La fécondité de cette démarche a à voir avec la recherche d'une perfection, avec la recherche du Beau. Avec la reconnaissance de la puissance et de la Sagesse de Dieu disait René-Just Haüy.